Что делать если вскочил флюс: Как вылечить флюс на десне без дальнейших осложнений? Расскажет АО СТОМАТОЛОГИЯ
Флюс после удаления зуба мудрости
Многие пациенты считают, что удаление больного зуба раз и навсегда избавит их от боли и мучений. Отчасти это действительно так. Однако утверждение верно только тогда, когда процедура экстракции была проведена качественно, а пациент соблюдал предписания врача в реабилитационный период. В противном случае новых проблем не избежать. Особенно неприятным осложнением, возникающим после удаления зуба, является флюс. О нем и пойдет речь в статье.
Причины возникновения флюса после экстракции
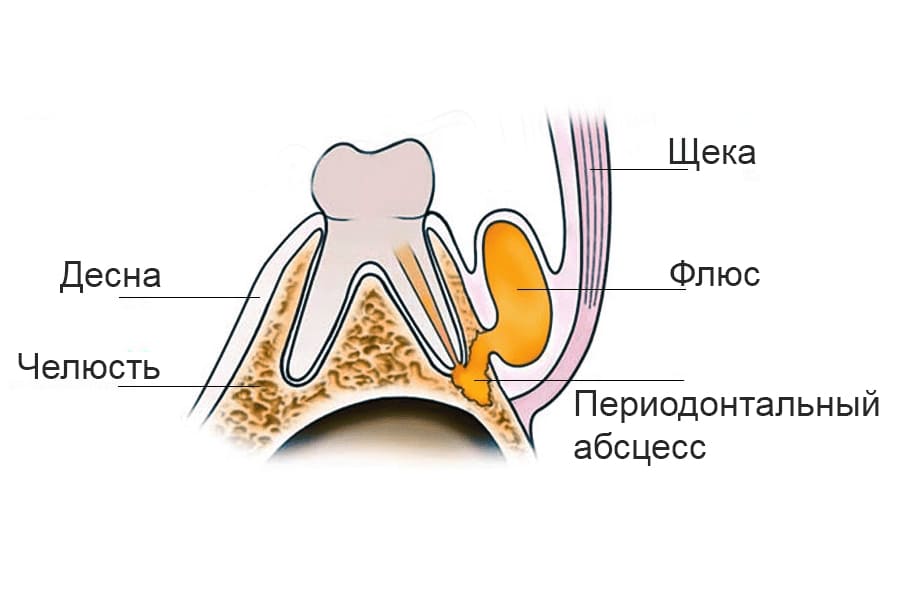
Под флюсом в стоматологии подразумевают воспалительный процесс, который формируется внутри мягких тканей и проявляется в виде опухания, гнойных выделений, повышенной температуры и других неприятных синдромов. Медицинский термин — периостит. Механизм развития флюса один: патогенные бактерии провоцируют развитие инфекции, которая по микроканальцам проникает внутрь десны и надкостницы.
Опасные симптомы!
- Глубокий воспалительный процесс.

- Инвазивное удаление зубов, после которого травмируется десна. Если не провести дополнительную противовоспалительную терапию, может развиться инфекция.
- Некачественный временный протез, который спровоцировал травму десны и попадание инфекции.
- Синдром сухой лунки.
Сколько держится флюс после удаления зуба?
Многие пациенты задаются вопросом, почему флюс после удаления зуба не проходит. Ответ на этот вопрос очевиден: если инфекция проникла глубоко в ткани и развился воспалительный процесс, удаление зуба вряд ли его остановит. Если же патология возникла непосредственно после экстракции, то рассчитывать на то, что проблема исчезнет самостоятельно, также не стоит. Разумеется, встречаются ситуации, когда начальное воспаление проходит благодаря защитным свойствам организма. Однако флюс — это итог, а не старт, поэтому сам по себе исчезнуть практически не может, даже если самостоятельно прорвется и часть гноя выйдет наружу.
Отек, температура и другие симптомы
Главный симптом, по которому визуально можно определить флюс, — это опухоль мягких тканей и характерный гнойный мешочек, который образуется в процессе развития патологии. Со временем клиническая картина ухудшается. К примеру, огромные опухоли на десне и на щеке — это результат периостита в тяжелой стадии. Один из характерных симптомов флюса — сильная боль, которая распространяется на обширный участок челюсти, а также отдает в ушах, шее и других участках головы. Температура после удаления зуба с флюсом (если он сохранился), как правило, стабильно высокая (от 38 градусов), однако в некоторых ситуациях температура тела не выходит за рамки нормальных показателей.
Внимание!
Важно понимать, что удаление зуба является хирургической манипуляцией. Воспаление, небольшое кровотечение и боль — вполне обыденное явление. Эти симптомы должны полностью пройти в течение нескольких дней. Если же боль держится более пяти дней, а также возникают вышеперечисленные проявления флюса, необходимо обратиться к лечащему врачу.
Лечение флюса после удаления зуба
Возник флюс после удаления зуба: что делать? Во-первых, нельзя затягивать с визитом к стоматологу. Чем раньше вы начнете лечение, тем выше шансы на скорое выздоровление. Врач оперативно поставит диагноз и составит оптимальный план реабилитации. Методика лечения флюса после удаления зуба зависит от тяжести патологии.Консервативное
Лечение проводится с помощью антибиотиков, которые подавляют активность бактерий. Антибиотики после удаления зуба с флюсом: Линкомицин; Ципрофлоксацин, Амоксиклав и их аналоги широкого спектра действия
Антибиотики после удаления зуба с флюсом: Линкомицин; Ципрофлоксацин, Амоксиклав и их аналоги широкого спектра действия
Наряду с антибиотиками назначаются противовоспалительные и обезболивающие препараты (Нимесил Диклофенак, Кетанов и др.). Справиться с воспалением помогают мази Метрогил Дента и Левомеколь. После удаления зуба с флюсом для очищения и защиты полости рта обязательны регулярные полоскания раствором Хлоргексидина, Мирамистина или соды (в случае отсутствия доступа к первым двум препаратам).
Внимание!
Перед применением необходима консультация организма.
Хирургическое
Если флюс находится на развитой стадии и произошло образование гнойного мешочка, наиболее действенной мерой является хирургическое вмешательство. Данная процедура носит название периостотомия. Врач стоматолог-хирург делает надрез в области воспаления, после чего устанавливает специальный дренаж для вывода гноя. Когда опухоль спадет и выйдет весь гной, пациенту накладывают швы. Хирургическое лечение не исключает прием антибиотиков и прочих вышеописанных противовоспалительных и антисептических средств.
Когда опухоль спадет и выйдет весь гной, пациенту накладывают швы. Хирургическое лечение не исключает прием антибиотиков и прочих вышеописанных противовоспалительных и антисептических средств.
Рекомендации по лечению и профилактике
Сколько держится флюс после удаления зуба, если своевременно начать лечение? На ранней стадии симптомы исчезают в течение двух-трех дней. При тяжелой форме (большой гнойный флюс после удаления зуба), когда требуется хирургическое вмешательство, реабилитация проходит дольше и занимает до нескольких недель. При этом важно то, как пациент соблюдает рекомендации врача и какие меры принимает для ускорения восстановления.
Запрещается!
- заниматься самолечением и самостоятельно назначать себе антибиотики;
- накладывать теплые компрессы и использовать разогревающие мази, так как это способствует размножению бактерий;
- пить аспирин перед хирургическим вмешательством, так как он разжижает кровь;
- в процессе восстановления запрещены активные физические нагрузки, походы в сауну и бассейн (даже когда челюсть уже не болит).

Флюс после удаления зуба мудрости возникает гораздо чаще, поскольку процедура удаления «восьмерок» обычно проходит весьма травматично, что сказывается на состоянии мягких тканей. После удаления зубов мудрости нужно особенно внимательно следить за своим состоянием и принимать все необходимые профилактические меры, чтобы минимизировать риск развития периостита.
Флюс
К сожалению, такое серьезное стоматологическое заболевание, как зубной флюс, встречается достаточно часто. В подавляющем большинстве случаев он требует хирургического вмешательства, что пугает пациентов, и обращение к врачу происходит достаточно поздно.
От чего появляется флюс и его виды
Для начала следует знать, что такое флюс зуба. Это гнойное образование – колония патогенных бактерий, которая в виде гранулемы располагается на корне зуба.
Флюс на щеке появляется не сразу. В случае если зуб, поврежденный кариесом, не лечится, бактерии проникают в зубной корень.
Существует два вида флюса – острый и хронический. Если вскочил флюс неожиданно, боль сильная, пульсирующая, повысилась температура, болит голова, опухоль большая – это его острый вид. Если, кажется, что флюс прошел, боль утихает, но опухоль остается и даже увеличивается, разговаривать больно, а потом все исчезает без вмешательства врачей – это хронический.
Может возникнуть флюс после удаления зуба, как реакция организма на вмешательство в структуру челюстной кости.
Как лечить?
Если образовался флюс, что делать может решить только стоматолог. Важно выяснить причину заболевания и провести правильное лечение флюса.
Не стоит думать, что для молочных зубов это заболевание менее опасно, флюс может повредить постоянный зубик, который находится под молочным. Когда появился флюс у ребенка, следует сразу обратиться в клинику. Не вылеченный флюс, возникший на десне, может стать причиной более серьезного заболевания. После профессионального удаления молочного зуба флюс проходит достаточно быстро.
Если для удаления флюса проводили операцию, вырвали зуб, обязательно по рекомендации стоматолога нужно полоскать ротовую полость, чтобы исключить осложнения. Кроме того, иногда стоматологи рекомендуют принимать антибиотики, чтобы избежать возникновения воспалительного процесса.
Флюс на десне после имплантации зубов
Содержание
Как заживает место имплантирования зуба
Восстановительный период включает:
- Образование кровяного сгустка, который защищает рану от инфекции.
 Он формируется в течение 10 дней.
Он формируется в течение 10 дней. - Разрастание соединительной ткани (грануляционной) — занимает до 4-х часов времени.
- Образование эпителия, восполняющего дефекты на месте повреждения. В среднем занимает 10 дней, сопровождается незначительным зудом.
- Восстановление и созревание поврежденных тканей. Начинается по истечении двух недель и продолжается до нескольких месяцев.
Симптомы флюса в области зубного импланта
Флюс, или периостит — плотное образование с гнойным содержимым. Имеет характерные признаки:
Обычно периостит затрагивает только десну, но в случае распространения воспаления
Причины развития заболевания после имплантации
- Инфицирование десны — инфекция попадает в рану после вживления и проникает в надкостницу. Область воспаления определить легко — на пораженном месте образуется болезненная шишка с гнойным содержимым.
 Появляется из-за:
Появляется из-за: - размножения бактерий при недостаточной гигиене;
- кариесогенной ситуации в ротовой полости;
- воспаления слизистой оболочки.
- Развитие периодонтита соседних зубов — заболевания, при котором воспаляются ткани периодонта с образованием нагноения. Начальная стадия болезни не представляет опасности.
- Периимплантит — флюс появляется при значительном воспалении десны, когда формируются десневые карманы. Это может свидетельствовать о развитии заболевания и нуждается в экстренном лечении.
- Инфекция внутренних органов — в редких случаях может стать причиной периостита. Группу риска составляют люди с ослабленным иммунитетом и часто болеющие острыми респираторными заболеваниями.
Методы лечения
Чтобы избавиться от флюса потребуется хирургическое вмешательство, предполагающее разрез десны и удаление гноя. Процедура состоит из следующих действий:
- Обезболивание.

- Надрез десны в области опухоли.
- Дренирование через надрез, удаление гноя.
- Обработка места рассечения антисептиком.
- Наложение дренажа на десну.
Дренаж позволяет полностью удалить гной и удерживает затягивание раны до полного удаления микроорганизмов. Дальнейшее лечение включает:
Растворы для полоскания должны использоваться не менее 3-х раз в день. Их можно приготовить самостоятельно или купить в аптеке — Мирамистин, Хлоргексидин.
Из рецептов народной медицины эффективны:
- Настой ромашки. Сбор заваривают, дают настояться и полощут ротовую полость. На стакан кипятка требуется 1 ч. ложка растения. Можно заваривать ромашку и цветки календулы в равном соотношении. Такая смесь кипятится 15 минут.
- Подорожник. Применяется в виде компресса из измельченных листов, отвара для полоскания. Сухое растение заливают водой, кипятят 15-20 минут, охлаждают и полощут рот.

- Календула. Настоянным отваром календулы полощут ротовую полость 3 раза в сутки.
Прием антибиотиков способствует уничтожению инфекции и позволяет избежать осложнений после хирургического вмешательства. Назначаются препараты из группы фторхинолонов, пенициллинов, линкозамидов:
- Амоксиклав — убивает патогенную микрофлору, провоцирующую воспалительные заболевания ротовой полости. Прием противопоказан при заболеваниях печени, лейкозе, непереносимости компонентов препарата.
- Линкомицин — антибиотик природного происхождения. Действует на грамположительные бактерии. Противопоказан при тяжелых заболеваниях печени, почек.
- Цифран — препарат на основе ципрофлоксацина. Эффективен в борьбе с бактериями, провоцирующими развитие периостита.
Курс лечения антибиотиками при периостите составляет до 10 дней. В этот период начинается восстановление тканей десны, продолжающееся около двух месяцев.
Какие еще осложнения возможны в послеоперационный период
Осложнения могут развиваться на фоне присутствия инфекции в ротовой полости, снижения иммунитета или недостаточного послеоперационного ухода. Разрез десны может повлечь:
- Отечность — нормальная реакция, возникает через пару часов после вмешательства и является следствием повреждения мягких тканей. Для снятия отеков к десне прикладывают лед. Припухлость тканей в течение недели не должна вызывать опасений. Если она не спадает и не уменьшается после допустимого периода, то существует большая вероятность воспаления.
- Повышенная температура — субфебрильная на протяжении 7 дней является нормальной реакцией. Температура выше 38 градусов, не спадающая на протяжении недели, в сочетании с отечностью десны, — это признаки воспалительного процесса.
- Болевые ощущения разной интенсивности — возникают после окончания действия анестетика и проходят через несколько дней.
 Показан прием обезболивающих препаратов по назначению врача. Непроходящая боль может свидетельствовать о развитии воспалительного процесса, повреждении нерва.
Показан прием обезболивающих препаратов по назначению врача. Непроходящая боль может свидетельствовать о развитии воспалительного процесса, повреждении нерва. - Кровотечение — допустима умеренная кровоточивость десны, но симптом должен исчезнуть в течение пары дней. Появление обильного кровотечения во время операции может возникнуть по причине низкой свертываемости крови или повышения артериального давления.
Длительное кровотечение может возникать при повреждении сосудов, что опасно развитием гематом. Гематомы тормозят процесс заживления, провоцируют нагноение раны, приводят к расхождению швов.
Что можно делать после операции, чего нельзя
Чтобы уберечься от осложнений, нужно выполнять врачебные рекомендации относительно приема медпрепаратов и общие рекомендации:
После операции нельзя делать согревающие компрессы, обрабатывать рану спиртом, раствором йода или бриллиантовым зеленым.
Удел незрячих | История, культура и традиции Рязанского края
Храм [Спаса на Нередице] выстроен крайне
небрежно, стены кривые, арки настолько
неровные, что иногда кажутся то ломаными,
то подковообразными… Новгородцы XI — XII
веков не были одарены творчеством в
архитектурной конструкции. Недаром
они потеряли и технические знания.
Некрасов А.И., искусствовед, специалист по древнерусской архитектуре
Ежели у тебя на щеке вскочил флюс,постарайся, чтобы такой же флюс вскочил и
на другой щеке, ибо ничто так не радует глаз,
как симметрия.
Козьма Прутков, виртуальный мудрец
Часть I.Что изучает история?
Отличная болезнь дальнозоркость! Видишь в мельчайших деталях то, что расположено у горизонта и в упор не замечаешь того, что находится у тебя под носом.
Редкой формой дальнозоркости страдают так называемые «профессиональные историки». В искусстве делать из объективных предпосылок ложные выводы им равных нет. Это в оружейном деле основной принцип «чем проще система, тем надёжнее она работает» — у историков всё наоборот. Варианты, лежащие на поверхности, лезущие в глаза, сами собой напрашивающиеся в качестве объяснения того или иного явления, ими отметаются, а на их место громоздятся нежизнеспособные, смехотворные теории, высосанные из пальца или откуда там они их высасывают. От того и свелась вся нынешняя «история» к – по меткому определению И. Стогова – коллекции битых горшков и бородатых анекдотов: «Что бы вы по этому поводу ни думали, современная наука «история» ни в каком смысле не является наукой. Сегодня за этим словом скрывается частично набор колотых горшков, частично – коллекция допотопных анекдотов, а по большей части – дырка от бублика. Никакой науки за этим словом не скрывается» (И. Стогов «Пепел империй»).
Это в оружейном деле основной принцип «чем проще система, тем надёжнее она работает» — у историков всё наоборот. Варианты, лежащие на поверхности, лезущие в глаза, сами собой напрашивающиеся в качестве объяснения того или иного явления, ими отметаются, а на их место громоздятся нежизнеспособные, смехотворные теории, высосанные из пальца или откуда там они их высасывают. От того и свелась вся нынешняя «история» к – по меткому определению И. Стогова – коллекции битых горшков и бородатых анекдотов: «Что бы вы по этому поводу ни думали, современная наука «история» ни в каком смысле не является наукой. Сегодня за этим словом скрывается частично набор колотых горшков, частично – коллекция допотопных анекдотов, а по большей части – дырка от бублика. Никакой науки за этим словом не скрывается» (И. Стогов «Пепел империй»).
Ладно бы, если современная история не была бы только наукой, но она даже и не лженаука – это, скорее, система догм и верований, своего рода религия. А современные историки, соответственно, это не профессия, а секта. Нравы её блестяще описал Кеннет Мак-Каллоч: «Многие дилетанты полагают, что главная задача учёных – поиск истины, и когда появляются новые факты и свидетельства, то учёные, естественно, должны пересмотреть свои прежние взгляды и переработать свои прежние построения. На самом же деле учёные могут быть столь же ограниченными приверженцами слепой веры, как и духовенство эпохи Средневековья» .
А современные историки, соответственно, это не профессия, а секта. Нравы её блестяще описал Кеннет Мак-Каллоч: «Многие дилетанты полагают, что главная задача учёных – поиск истины, и когда появляются новые факты и свидетельства, то учёные, естественно, должны пересмотреть свои прежние взгляды и переработать свои прежние построения. На самом же деле учёные могут быть столь же ограниченными приверженцами слепой веры, как и духовенство эпохи Средневековья» .
О деятельности секты «историков» можно сказать, что на современном этапе она сводится к двум вещам: во-первых, сохранению устоявшегося набора стереотипов в неизменном виде и, во-вторых, агрессивной обороне от чужаков или собственных вероотступников, пытающихся докопаться до истины. Не верите? Пожалуйста, пример…
Возьмём самый известный мировой артефакт – египетские пирамиды. «История» начала изучать их с того самого дня, как вылупилась на свет – и что?! Что нам могут поведать господа «историки» про пирамиды? Ни-че-го! Ни кто их построил, ни когда построил, ни зачем построил… ну, уж, а про то, как построил, вообще, спрашивать стыдно!
Всех познаний современной «истории» о пирамидах Гизы едва наскреблось вот на эту примитивную схему для туристов – да, и в той полно ошибок.
Позвольте, а на что же растрачены многомиллионные спонсорские гранты, с завидным постоянством выделяемые египтологам со времён Наполеона? А на то и растрачены… Первая половина на то, чтобы во всех без исключения школьных учебниках была напечатана одна и та же «общепринятая» версия про то, что пирамиды были врукопашную возведены около 2500 года до нашей эры толпами голодных рабов. Вторая – на борьбу с критиками упомянутой версии. Вот и вся «история»!
Собственно история, которую можно писать без кавычек и не стыдно называть наукой, начинается везде в тот момент, когда с раскопок выгоняют поганой метлой «профессиональных историков» и приглашают на их место людей, чьи профессии от истории на первый взгляд кажутся далёкими. И их заключения сметают нелепые теории «историков», как бульдозер карточный домик.
В случае с хрестоматийными пирамидами всё началось, например, не с «историков», которых вполне устраивала «каноническая» версия про трудовые армии рабов, вооружённых медными зубилами, а, вообще, с врачей. Втемяшилось неким биохимическим умам выяснить рецепт бальзама, которым бальзамировали мумии фараонов. Для практической медицины, надо сказать, пользы от этого никакой, но на случай сохранения для потомков чучела очередного ильича вполне даже может пригодиться. А потому пытливые медики отпилили от ненужной мумии кусочек, растолкли его в ступке, добавили какие надо реактивы и полученную кашицу поместили в колонку хроматографа. А когда хроматограф изрыгнул из недр своего искусственного интеллекта заключение о составе бальзамирующей смеси, врачам оставалось только присвистнуть – в состав бальзама входило эвкалиптовое масло. Эвкалипты, как известно, растут только в Австралии и нигде более, а Австралию, как ошибочно считает «академическая версия» открыл в 1606 году нашей эры голландец Биллем Янзсон. От комментариев по поводу, каким образом эвкалиптовое масло попало в мумию фараона и не стоит ли внести кое-какие коррективы в свои узколобые представления о кругозоре древних египтян «профессиональные историки» воздержались.
Втемяшилось неким биохимическим умам выяснить рецепт бальзама, которым бальзамировали мумии фараонов. Для практической медицины, надо сказать, пользы от этого никакой, но на случай сохранения для потомков чучела очередного ильича вполне даже может пригодиться. А потому пытливые медики отпилили от ненужной мумии кусочек, растолкли его в ступке, добавили какие надо реактивы и полученную кашицу поместили в колонку хроматографа. А когда хроматограф изрыгнул из недр своего искусственного интеллекта заключение о составе бальзамирующей смеси, врачам оставалось только присвистнуть – в состав бальзама входило эвкалиптовое масло. Эвкалипты, как известно, растут только в Австралии и нигде более, а Австралию, как ошибочно считает «академическая версия» открыл в 1606 году нашей эры голландец Биллем Янзсон. От комментариев по поводу, каким образом эвкалиптовое масло попало в мумию фараона и не стоит ли внести кое-какие коррективы в свои узколобые представления о кругозоре древних египтян «профессиональные историки» воздержались.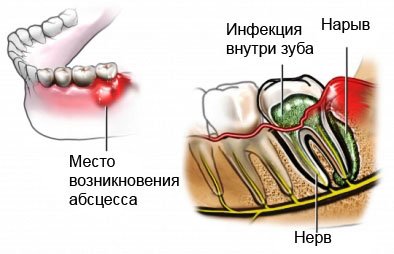 Не получив вразумительных объяснений в отношении выявленного факта у профессиональных хранителей исторического наследия, врачам ничего не осталось, как обратиться к собратьям-биологам.
Не получив вразумительных объяснений в отношении выявленного факта у профессиональных хранителей исторического наследия, врачам ничего не осталось, как обратиться к собратьям-биологам.
Биологи поступили ещё проще: купили на ближайшем рынке полкило свежего мяса и яблоко. И то, и другое разрезали пополам. Одни половины оставили дома, а вторые отнесли в пирамиду и спрятали в укромном местечке. Сравнивая глубину и скорость процессов происходящих с аутентичными частями мяса и яблока, биологи даже без хроматографа выяснили, что мясо в пирамиде не протухает, а яблоко не гниёт. Когда оставленные дома фрагменты уже покрылись опарышами, их половины, заточённые в пирамиде, представляли собой усохшие до степени мумификации, но вполне пригодные к употреблению продукты. Немного уклонившись от темы, позволю себе привести ещё один занимательный факт: найденные в пирамиде зёрна пшеницы, возрастом около 5 тысяч лет, при посеве проросли и дали вполне приемлемые показатели урожайности. У «профессиональных историков» опять объяснений не появилось, а биологических знаний для этого уже стало не доставать. Биологи предположили, что может дело не в самой пирамиде, а в материале, из которого она сделана – мало ли, радиация, там, или что ещё похуже! – и позвали на помощь геологов.
Биологи предположили, что может дело не в самой пирамиде, а в материале, из которого она сделана – мало ли, радиация, там, или что ещё похуже! – и позвали на помощь геологов.
Геологи постучали своими молоточками и выдали резюме: нет, камень как камень – ничего выдающегося. Только… как бы объяснить… сложены гизехские пирамиды из гранита и базальта. Гранит брали в Асуане, а вот базальт… короче, нет в Египте месторождения, откуда могли брать такой базальт… и во всей Африке нет… и не известно ещё есть ли вообще таковое на нашей грешной планете. Да, кстати, эрозия на камнях какая-то нетипичная для здешних мест – с климатологами посоветуйтесь.
Климатологи бегло взглянули на пирамиды, на Сфинкса и пожали плечами: а что такого? Нормальная такая вполне эрозия. Правда, она не горизонтальная ветровая, а вертикальная дождевая и свидетельствует о том, что пирамиды и Сфинкс стояли уже тогда, когда Египет ещё заливали ливни, а было это 10000 лет назад минимум, во времена ледниковые… Ну, а то, что это с «общепринятыми» датировками пирамид 2500-м годом до Рождества Христова не вяжется – так это проблемы тех, кто эти датировки нафантазировал.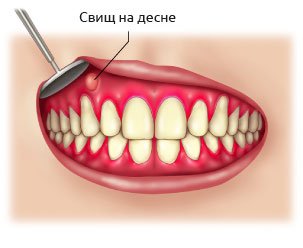 Зовите-ка физиков.
Зовите-ка физиков.
Тёмные потёки на лице Сфинкса – следы вертикальной дождевой эрозии.
Физики первым делом установили, что пирамиды «гасят» все внешние электро-магнитные влияния, поэтому внутри пирамид не «ловят» мобильные телефоны и даже не работают куда более мощные полицейские рации. Зато пирамиды генерируют какое-то своё поле, поэтому беспорядочно рассыпанные металлические опилки внутри них ориентируются, а тупые бритвы самозатачиваются. «Профессиональные историки» на полученные данные опять ответили массовым молчанием, а физики предположили, что пирамиды – это не просто отдельно стоящие строения, а части какой-то масштабной геофизической системы. Пригласили геодезистов.
Геодезисты тоже порадовали: пирамиды Гизы оказались ориентированы по оси север-юг с точностью 0,015%. Факт этот примечателен даже для нашей цивилизации, вооружённой компьютерами, лазерными дальномерами, оптическими теодолитами и спутниковыми системами позиционирования. А для цивилизации Бронзового века, не знавшей, что Земля круглая, такая точность немыслима.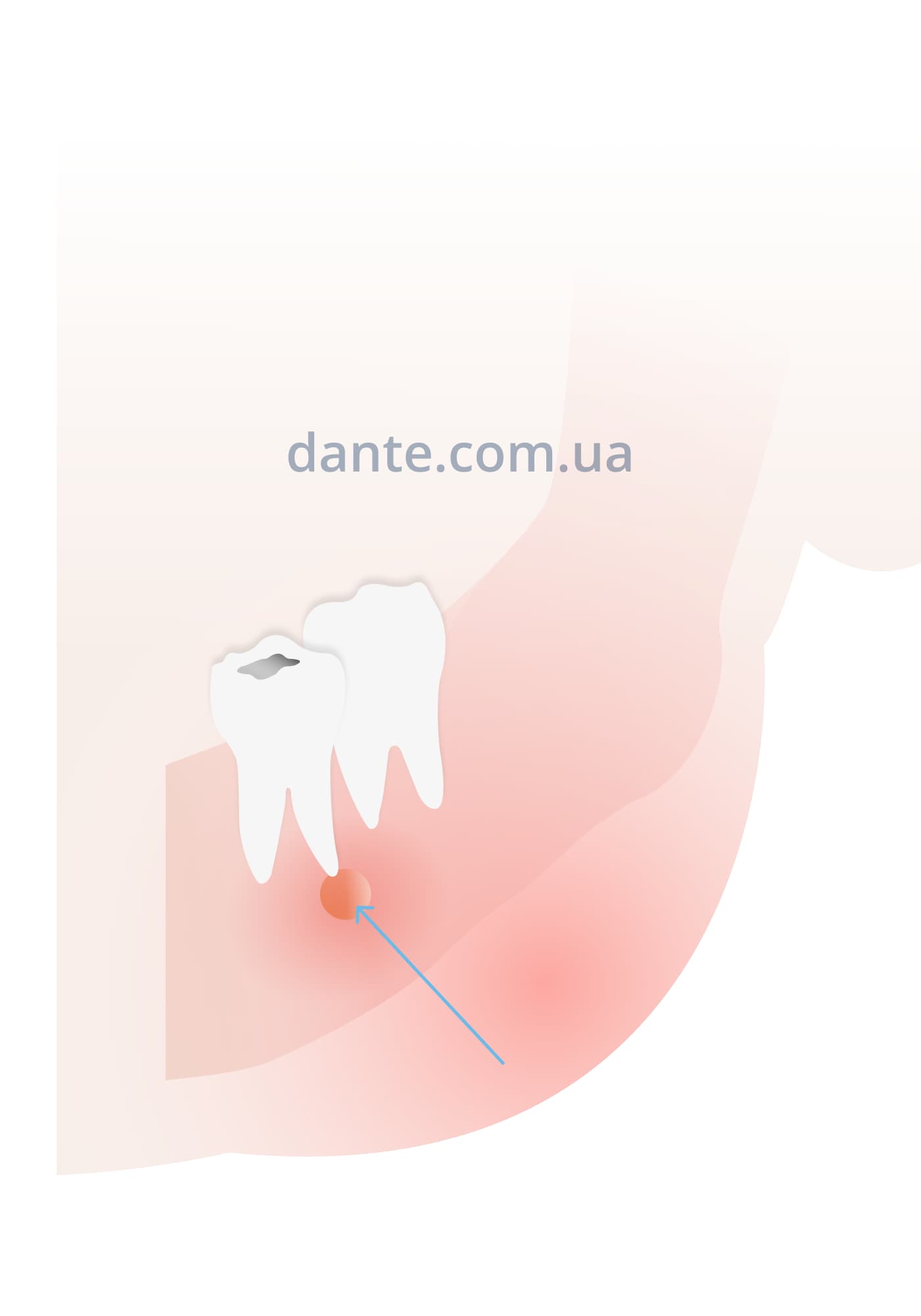 Немыслима и, к тому же, бесполезна, поскольку невооружённый человеческий глаз не воспринимает отклонения даже в 1%. Ну, а поскольку, не имея компьютеров и навигационных спутников, выставить объект по сторонам света с такой точностью можно только по светилам, то геодезисты посоветовали пригласить астрономов.
Немыслима и, к тому же, бесполезна, поскольку невооружённый человеческий глаз не воспринимает отклонения даже в 1%. Ну, а поскольку, не имея компьютеров и навигационных спутников, выставить объект по сторонам света с такой точностью можно только по светилам, то геодезисты посоветовали пригласить астрономов.
Пирамиды идеально ориентированы по оси север-юг, Сфинкс (указан стрелкой) – столь же идеально ориентирован по оси восток-запад.
Пришли астрономы. Посмотрели сначала на пирамиды, потом на небо, потом опять на пирамиды – всё понятно. Сфинкс смотрит на точку восхода Солнца в дни равноденствий, а пирамиды представляют собой проекцию на земную поверхность Пояса Ориона. Именно, проекцию, а не схему, так как выдержаны не только взаиморасположение и видимые величины звёзд, но и пропорции расстояний между ними.
Компьютерное совмещение звёзд, образующих Пояс Ориона, и пирамид Гизы.
Да, кстати, у вас там, – это астрономы к «историкам» обращаются – внутри пирамиды есть то, что вы называете «восточная шахта камеры царя» . Что это такое мы, как и вы, не знаем, но точно, что оно нацелено на Аль-Нитак – нижнюю звезду Пояса Ориона. А такая же шахта «камеры царицы» смотрит на Тубан… он же альфа Дракона… он же Полярная звезда эпохи с 3500 по 1500 года до нашей эры… Такого «профессиональные историки» уже стерпеть не смогли и всё историческое стадо взорвалось возмущённым блеянием!
Что это такое мы, как и вы, не знаем, но точно, что оно нацелено на Аль-Нитак – нижнюю звезду Пояса Ориона. А такая же шахта «камеры царицы» смотрит на Тубан… он же альфа Дракона… он же Полярная звезда эпохи с 3500 по 1500 года до нашей эры… Такого «профессиональные историки» уже стерпеть не смогли и всё историческое стадо взорвалось возмущённым блеянием!
В этом месте надо сделать лирическое отступление для того, чтобы сказать, что к астрономии «профессиональные историки» питают особые чувства. С одной стороны отмахнуться от факта наличия у древних цивилизаций феноменальных астрономических знаний нельзя, но с другой стороны именно он, этот факт, больнее всего бьёт по основной «исторической концепции»: мы – умные и красивые, а все, кто были до нас – дикари и варвары. Просто, одно дело пусть исключительно сложный и недоступный пониманию объект на Земле – его как-то ещё можно списать на трудовой порыв армии рабов, подхлёстнутый дурью желающего увековечить свои комплексы фараончика. И совсем другой разговор, если это вопросы устройства дальнего космоса и Вселенной в целом. Это уже категории другого порядка никакими сказками про массовые религиозно-экстатические радения не объясняемые. А признать, что в вопросах мироустройства те же древние египтяне или шумеры разбирались лучше нас, нынешних, это означает признать полную несостоятельность того, что мы называем «историей». Поэтому-то «профессиональные историки» в упор не видят или не желают видеть явных астрономических мотивов, даже там, где они просто вопиют о себе.
И совсем другой разговор, если это вопросы устройства дальнего космоса и Вселенной в целом. Это уже категории другого порядка никакими сказками про массовые религиозно-экстатические радения не объясняемые. А признать, что в вопросах мироустройства те же древние египтяне или шумеры разбирались лучше нас, нынешних, это означает признать полную несостоятельность того, что мы называем «историей». Поэтому-то «профессиональные историки» в упор не видят или не желают видеть явных астрономических мотивов, даже там, где они просто вопиют о себе.
Пример пирамид самый показательный, но – увы! – не единичный. Пирамиды, если верить книге рекордов Гиннеса, самый фотографируемый объект на планете Земля. Второе место по этому критерию принадлежит Стоунхенджу. И что же знает современная «история» про Стоунхендж? Да, то же, что и про пирамиды!
Стоунхендж.
Первым изучать Стоунхендж на научной основе взялся король Яков I ещё в 1620 году. Инспектируя свои владения, монарх был раздражён кучей гигантских камней, портящих вид зелёных ландшафтов Вилтшира. Тут же придворному архитектору Индиго Джонсу последовал приказ разобраться, что это такое и зачем оно тут нагромождено. Джонс описал два круга: внутренний из пяти трилитов, и внешний из тридцати каменных глыб весом по 20-25 тонн каждая. Многие из них уже были повалены, но круговая планировка читалась довольно ясно. Джонс сделал заключение, что Стоунхендж – это развалины некоего храма, построенного римлянами во время оккупации ими Британии. Вы удивитесь, но, несмотря на явную несуразность, среди наиболее упёртых мракобесов эта протухшая схоластика ещё используется в качестве теории – загляните, хотя бы в Википедию! Это называется – на костёр пойду, а тремя перстами не перекрещусь!
Тут же придворному архитектору Индиго Джонсу последовал приказ разобраться, что это такое и зачем оно тут нагромождено. Джонс описал два круга: внутренний из пяти трилитов, и внешний из тридцати каменных глыб весом по 20-25 тонн каждая. Многие из них уже были повалены, но круговая планировка читалась довольно ясно. Джонс сделал заключение, что Стоунхендж – это развалины некоего храма, построенного римлянами во время оккупации ими Британии. Вы удивитесь, но, несмотря на явную несуразность, среди наиболее упёртых мракобесов эта протухшая схоластика ещё используется в качестве теории – загляните, хотя бы в Википедию! Это называется – на костёр пойду, а тремя перстами не перекрещусь!
В английской народной традиции строительство Стоунхенджа приписывается легендарному волшебнику Мерлину, которому помогали великаны.
Другой любопытный король Карл II в 1678 году поручил знатоку древностей Джону Обри повторно исследовать руины. Обри, помимо двух кругов мегалитов, обнаружил ещё один круг, составленный из 56 углублений, которые с тех пор носят его имя – лунки Обри. Кроме того, Обри вынес вердикт, что к римлянам строение не имеет никакого отношения, а представляет собой кельтское святилище.
Кроме того, Обри вынес вердикт, что к римлянам строение не имеет никакого отношения, а представляет собой кельтское святилище.
Астрономические мотивы в Стоунхендже первым уловил Джон Вуд. В 1740 году он предположил, что Стоунхендж был «храмом друидов, посвященным Луне» . В том же году Уильям Стакли установил, что центральная ось всего сооружения, проходящая через Алтарный камень, Пяточный камень и направленная вдоль Аллеи, ориентирована на точку, совпадающую с положением восходящего Солнца в период летнего солнцестояния.
Прохождение лучей Солнца сквозь расщелину Пяточного камня и их падение на Алтарный камень в день летнего солнцестояния (схема).
В 1901 году директор обсерватории в Саунт-Кенсингтоне сэр Джозеф Норманн Локьер впервые высказал идею о том, что Стоунхендж – это не столько храм, сколько пригоризонтная обсерватория. По собственной методике, с использованием астрономических методов, Локьер датировал возведение сооружения 1860 плюс-минус 200 лет годом до нашей эры (по самым последним данным – археологический сезон 2008 года, экспедиция под руководством Майкла Паркера Пирсона – окончание строительства Стоунхенджа радиоуглеродным методом датировано 1900 годом до нашей эры! ), то есть отнёс его глубоко к докельтской эпохе. За столь смелые заявления Локьер подвергся даже не обструкции, а форменной травле, доведшей учёного до могилы.
За столь смелые заявления Локьер подвергся даже не обструкции, а форменной травле, доведшей учёного до могилы.
В 1923 году по поручению Королевской британской службы мер и весов доктор Александр Том обследовал Стоунхендж. Том установил, что камни для его строительства брались с месторождения в горах Прескелли (220 км. – по прямой, 380 км. – в объезд) и робко предположил, что теория Локьера относительно астрономического назначения Стоунхенджа может оказаться верной. Последнее привело к тому, что заказчик исследований от услуг Тома отказался.
Следующий этап мытарств вокруг Стоунхенджа стал переломным и случился в 1963 году, когда астроном Смитсоновской астрофизической обсерватории (Массачусетс, США) Джеральд Хоукинс опубликовал в журнале «Nature» статью, где на основе компьютерного анализа 7140 возможных вариантов прохождения визуальных линий, доказал, что Стоунхендж – это обсерватория высокого для своего уровня класса, позволяющая решать целый комплекс астрономических задач. Идеи статьи впоследствии Хоукинс развил в полноценную теорию, изложенную в книге «Разгадка тайны Стоунхенджа».
Идеи статьи впоследствии Хоукинс развил в полноценную теорию, изложенную в книге «Разгадка тайны Стоунхенджа».
Хоукинс за свои взгляды был «официальной наукой» предан анафеме и объявлен шарлатаном. Больше всех отличился в поливании его помоями профессор Кардифского университета Уэльса Ричард Аткинсон, издавший контр-книгу «Лунный блик на Стоунхендже», где осмеял и Локьера, и Тома, и Хоукинса.
Гигантские каменные блоки весом по 20-25 тонн были не просто нагромождены друг на друга, а скреплялись сложной системой пазов и шарниров – «официальная история» утверждает, что основным инструментом строителей Стоунхенджа были костяные копалки из оленьих рогов…
Однако, Хоукинс своё дело уже сделал – прогрессивные умы всколыхнулись. Внезапно на Стоунхендж вернулся капитулировавший было Александр Том. Как выяснилось, от своих взглядов он не отрёкся, а наоборот подготовил ортодоксам от истории целую подборку зубодробительных аргументов. Том изучил более 600 близких по возрасту и концепции мегалитических строений, установил, что их строители от Камбоджи до Ирландии пользовались единой эталонной единицей длины – мегалитическим ярдом – и обнаружил их астрономическую мотивацию: «Трудно представить себе, чтобы строители эпохи мегалита могли спланировать и возвести свои монументальные постройки, не обладая этими [астрономическими] знаниями, а между тем такие знания явно налицо… Мы не знаем, в какой мере эти познания связаны с их прочими представлениями о мире, но, какими бы мотивами они ни руководствовались, математические принципы, воплощённые в их творениях, сами по себе достаточно важны и вызывают доверие к этим камням».
«Историческое сообщество» в очередной раз окрысилось, но отмахнуться от выкладок Тома уже не смогло. Даже случилось чудо – упомянутый профессор Аткинсон, поносивший Тома в своём памфлете «Лунный блик на Стоунхендже», раскаялся и перешёл в новую веру, защищать которую стал с тем же энтузиазмом, с каким ранее громил. Свою метаморфозу он сам объяснил так:
Работа Тома опрокидывала концептуальную модель предыстории Европы, бывшую общепризнанной все нынешнее столетие и только теперь начинающую трескаться по краям…В условиях этой модели просто непредставимо, как обычные варвары на отдаленных окраинах северо-востока континента могли обладать знаниями математики и ее применения, едва ли меньшими, чем в Египте того же времени или Месопотамии значительно более поздней эпохи.
Поэтому едва ли удивительно, что многие исследователи первобытного общества или игнорировали следствия работы Тома, потому что не понимали их, или же сопротивлялись им потому, что так было гораздо спокойней.
 Я сам прошел через второй путь; но пришел к заключению, что если отвергать тезис Тома из-за того, что он не вписывается в модель предыстории, на которой я был воспитан, то придется признать невероятности и гораздо высшего порядка.
Я сам прошел через второй путь; но пришел к заключению, что если отвергать тезис Тома из-за того, что он не вписывается в модель предыстории, на которой я был воспитан, то придется признать невероятности и гораздо высшего порядка. И что бы вы думали?! Что порыв Ричарда Аткинсона был подхвачен остальными историками и они, со слезами ударяя себя в грудь, покаялись в умышленной лжи, которую выдавали нам под торговой маркой «История©» и публично отказались от незаслуженных учёных степеней и регалий? Не тут-то было! Подавляющая часть «исторического сообщества» насмерть встала на защиту абсурдных, но удобных «общепризнанных» теорий. А Истина в очередной раз оказалась принесённой в жертву амбициям: «Еще авторы XVIII века подметили, что положение камней можно увязать с астрономическими явлениями. Наиболее известная современная попытка истолкования Стоунхенджа как грандиозной обсерватории каменного века принадлежит Дж. Хокинсу и Дж. Уайту. Поддержки в современном научном сообществе эта гипотеза практически не имеет» — гласит Википедия.
Они всё те же – только рясы сменили на пиджаки и прикрываются теперь не именем божьим, а «академическими версиями»…
Стоунхендж мракобесов от науки не убедил… не убедили их и многочисленные однотипные обсерватории, открытия которых посыпались после книги Хоукинса как из рога изобилия. В трёх километрах от Стоунхенджа был обнаружен его деревянный аналог – Вудхендж. В Шотландии – Калланиш. В Ирландии – Нью-Грейндж. Во Франции – Карнак. В Германии – Голоринг под Кобленцом и Гозекский камень в Гозеке (к слову, всего в Германии выявлено более 250 таких сооружений). В Дании – Треллеборг, Фиркат, Эскехольм и Аггерсборг. Найдены «стоунхенджи» в Австрии, Чехии, Польше, Украине, на Мальте. Есть они и у нас, в Рязанской области, прямо под носом – это недавно открытая деревянная обсерватория, получившая в прессе название «Рязанский Стоунхендж» (наш сайт писал о нём неоднократно: http://history-ryazan.ru/node/212; http://history-ryazan.ru/node/6281).
Схематическая реконструкция «Рязанского Стоунхенджа».

Быть может, опережая события, скажу, что в нашей области, на Михайловской трассе, на берегу реки Жраки есть ещё один загадочный кольцевидный объект, очень концептуально напоминающий вышеперечисленные сооружения. К сожалению, наш «Жракахендж» пока обойдён вниманием учёных, но кто знает, какие сюрпризы преподнесёт его детальное изучение.
Кольцевидный объект – это и есть ждущий своего признания Жракахендж (ну, летом кто со мной?!).
Не могу удержаться, чтобы не похвалить сам себя! Все перечисленные мною объекты мало того, что имеют внешнее, принципиальное и функциональное сходство, так ещё и расположены практически на одной широте. Этот, тоже, кстати, «официальной наукой» не объяснённый феномен я детально разбирал в собственном исследовании «Код Петра Великого».
Средний:Рейтинг: 5 (5 голосов)
Используйте Flux для группировки, формирования и анализа данных временных рядов
Flux — это язык программирования, разработанный с нуля для анализа временных рядов. Традиционно группировка, формирование и выполнение математических операций над большими наборами данных динамических временных рядов являются громоздкими. Цель Flux — сделать работу с этими наборами данных более элегантной.
Традиционно группировка, формирование и выполнение математических операций над большими наборами данных динамических временных рядов являются громоздкими. Цель Flux — сделать работу с этими наборами данных более элегантной.
В альфа-версию InfluxDB 2 OSS было добавлено несколько новых интересных функций Flux, которые заставили меня прыгнуть с двух ног, чтобы увидеть, как они будут работать на практике.Мой первоначальный набег был многообещающим, но что-то пошло не так.
Мой ключ к пониманию Flux
Изучая, как анализировать данные из нескольких хранилищ данных, я быстро понял, что упускаю что-то фундаментальное. Я продолжал получать неожиданные ответы, и многие из моих графиков сбились.
В поисках ответов я обратился к Адаму Энтони из команды Flux, и он шаг за шагом провел меня через более сложный вариант использования. Через несколько шагов это щелкнуло — ключевой частью, на которую я должен был обратить пристальное внимание, были результаты таблицы.
Таблицы как данные
Первые несколько примеров, с которыми вы сталкиваетесь во Flux, кажутся очень простыми. Это типичный первый запрос, который вы можете увидеть в системных метриках, собранных локальным агентом телеграфа:
. из(ведро:"мое-ведро")
|> диапазон (начало: -10 м)
|> filter(fn: (r) => r._measurement == "cpu" и r._field == "usage_system" и r.cpu != "cpu-total" ) Этот запрос Flux извлекает все данные, которые агент Telegraf записал в my-bucket за предыдущие десять минут, и фильтрует их до показателей использования системы ЦП, исключая общие значения ЦП.
Когда я впервые увидел результат этого запроса в своем пользовательском интерфейсе InfluxDB Cloud 2, я пришел к выводу, что Flux просто возвращает четыре массива, каждый из которых содержит множество чисел. Оказывается, это первоначальное впечатление было очень неверным и стало причиной моих ошибок при попытке решить более сложные сценарии.
После уроков Адама я понял, что использование и понимание Flux зависит от понимания каждой части результатов Flux. Результаты Flux представляют собой таблицы, и иногда результаты представляют собой довольно обширный набор таблиц.Я узнал, что самый полезный инструмент, на который можно опереться при переходе к анализу Flux, — это не инструмент построения графиков, а переключатель пользовательского интерфейса для просмотра необработанных данных.
Результаты Flux представляют собой таблицы, и иногда результаты представляют собой довольно обширный набор таблиц.Я узнал, что самый полезный инструмент, на который можно опереться при переходе к анализу Flux, — это не инструмент построения графиков, а переключатель пользовательского интерфейса для просмотра необработанных данных.
Представление Raw — это именно то, что нужно — полный необработанный вывод Flux. Когда я впервые посмотрел на необработанное представление, я подумал, что, возможно, пользовательский интерфейс добавляет такие вещи, как метки, временные метки или расширенные описания. На самом деле пользовательский интерфейс ничего не добавляет к результату — каждая метка, строка и столбец здесь взяты прямо из ответа Flux.
Копаясь в ответе, легче всего упустить из виду столбец таблицы — третий столбец в этом примере.Приведенный выше пользовательский интерфейс прокручивается для отображения данных из двух таблиц (таблица 0 и таблица 1). Мы видим, что приведенный выше запрос Flux системного процессора вернул вовсе не четыре массива, а четыре таблицы — по одной таблице для каждого из четырех процессоров, которые отслеживает Telegraf.
Когда вы манипулируете, анализируете и формируете свои данные, если вы будете помнить о том, что каждый промежуточный расчет и результат представляет собой таблицу, вы окажетесь намного ближе к ответам, которые ищете. В последнем примере ниже рассматривается более сложный вариант использования, чтобы продемонстрировать шаг к ответу, сосредоточив внимание на таблицах.
Повторное посещение поставщика здоровья аквариума
Давайте продолжим пример использования поставщика данных о состоянии аквариума, который хранил метаданные IoT в Postgres, а данные датчиков — в InfluxDB. В этом примере поставщик хотел, чтобы его представители по работе с клиентами знали балансы pH во всех аквариумах клиента. После соединения результат таблицы выглядел так:
Этот результат достаточно прост для прочтения и усвоения менеджером по работе с клиентами, но добавьте пару десятков резервуаров и датчиков, и представители будут плавать в данных.Чтобы упростить задачу, руководство поняло, что торговым представителям действительно нужно знать расположение аквариумов с pH выше 8.
К счастью, они используют Flux и могут использовать великолепный встроенный оператор переадресации конвейера, чтобы просто использовать первоначальный результат таблицы выше в дополнительных вычислениях, чтобы найти самое высокое среднее значение pH.
// сгруппировать по местоположению, чтобы мы могли анализировать каждое местоположение независимо от других. (создает 3 таблицы из 1)
|> группа (столбцы: ["customer_location"]) // найти среднее значение внутри каждой таблицы
|> среднее (столбец: "_value") // группировка без столбцов объединяет все таблицы в одну таблицу
|> группа(столбцы: []) // отфильтровать все строки данных ниже значения 8
|> filter(fn: (r) => r._значение > 8) // отсортировать список, чтобы аквариумы с наивысшим приоритетом находились вверху списка
|> sort(столбцы: ["_value"], описание: true) После обработки и фильтрации всех данных специалист по работе с клиентами должен иметь управляемый список аквариумов, на которых следует сосредоточиться. В этом случае в верхней части списка находится аквариум в вестибюле, который, похоже, требует серьезного внимания.
В этом случае в верхней части списка находится аквариум в вестибюле, который, похоже, требует серьезного внимания.
У Flux светлое будущее
Flux начинает набирать обороты, поскольку выпускаются многие мощные функции, такие как условные операторы и хранилища с несколькими данными.Сейчас самое подходящее время, чтобы перейти и внимательно изучить Flux, если вы занимаетесь любыми вариантами использования анализа временных рядов. Легко начните работу, подписавшись на InfluxDB Cloud 2 или загрузив последнюю альфа-версию OSS.
Как всегда, если у вас есть вопросы или пожелания по Flux, зайдите на форум сообщества Flux и сообщите нам об этом.
Скачки потока в кольцеобразных и сборных объемных сверхпроводниках при намагничивании импульсным полем
Цитата
Чжоу, Д., Ши Ю., Деннис Т., Кардуэлл Д. и Даррелл Дж. (2020). Скачки потока в кольцеобразных и сборных объемных сверхпроводниках при намагничивании импульсным полем. Наука и технологии сверхпроводников, 33 (3) https://doi. org/10.1088/1361-6668/ab66e7
org/10.1088/1361-6668/ab66e7
Аннотация
 Такое поведение объясняется различными эффектами, в том числе неоднородностью материала, которая может привести к образованию локальных горячих точек во время процесса PFM. Для дальнейшего выяснения этого явления были изучены свойства структуры, состоящей из объемного сверхпроводящего кольца с цилиндрическим сверхпроводниковым сердечником. Мы наблюдаем, что, хотя в кольце последовательно происходит скачок потока, на границе кольцеобразного образца и ядра устанавливается критическое состояние.Мы предоставляем подробный отчет об этих экспериментальных наблюдениях и даем объяснение с точки зрения текущего понимания процесса PFM.
Такое поведение объясняется различными эффектами, в том числе неоднородностью материала, которая может привести к образованию локальных горячих точек во время процесса PFM. Для дальнейшего выяснения этого явления были изучены свойства структуры, состоящей из объемного сверхпроводящего кольца с цилиндрическим сверхпроводниковым сердечником. Мы наблюдаем, что, хотя в кольце последовательно происходит скачок потока, на границе кольцеобразного образца и ядра устанавливается критическое состояние.Мы предоставляем подробный отчет об этих экспериментальных наблюдениях и даем объяснение с точки зрения текущего понимания процесса PFM.
Права
Все права защищены
Лицензия:
http://www.rioxx.net/licenses/all-rights-reserved
%PDF-1.4
%
1 0 объект
>
эндообъект
6 0 объект /Заголовок
/Предмет
/Автор
/Режиссер
/Ключевые слова
/CreationDate (D:20220202014556-00’00’)
/Заявитель (пакет StampPDF 4.5.1, 16 ноября 2007 г.)
/ModDate (D:20211001095549+01’00’)
/СПДФ (1122. 1)
>>
эндообъект
2 0 объект
>
эндообъект
3 0 объект
>
эндообъект
4 0 объект
>
эндообъект
5 0 объект
>
ручей конечный поток
эндообъект
7 0 объект
>
эндообъект
8 0 объект
>
эндообъект
9 0 объект
>
эндообъект
10 0 объект
>
эндообъект
11 0 объект
>
эндообъект
12 0 объект
>
эндообъект
13 0 объект
>
эндообъект
14 0 объект
>
/ProcSet [/PDF /Text /ImageC /ImageB /ImageI]
>>
эндообъект
15 0 объект
>
ручей
xڝYɎ6+HfF,HnAЮJA0~rdFdQHOTr:>O~2}|C0torp&zK\2 ?^~~xy-,srA9Sr’1\$|C;%k[B
?L8x и wsuճsC
1)
>>
эндообъект
2 0 объект
>
эндообъект
3 0 объект
>
эндообъект
4 0 объект
>
эндообъект
5 0 объект
>
ручей конечный поток
эндообъект
7 0 объект
>
эндообъект
8 0 объект
>
эндообъект
9 0 объект
>
эндообъект
10 0 объект
>
эндообъект
11 0 объект
>
эндообъект
12 0 объект
>
эндообъект
13 0 объект
>
эндообъект
14 0 объект
>
/ProcSet [/PDF /Text /ImageC /ImageB /ImageI]
>>
эндообъект
15 0 объект
>
ручей
xڝYɎ6+HfF,HnAЮJA0~rdFdQHOTr:>O~2}|C0torp&zK\2 ?^~~xy-,srA9Sr’1\$|C;%k[B
?L8x и wsuճsC
Flux интерфейс. Раздел: NewColorPicker (тема «Измени свой». К счастью, Flux означает
Раздел: NewColorPicker (тема «Измени свой». К счастью, Flux означает
 Управление активами — как для управляющих активами, так и для институциональных инвесторов — становится все более сложной задачей.Возвращение настоящего визуального дизайнера RAD для всего дизайна пользовательского интерфейса в Visual Studio приведет к стремительному развитию C# и . Если вашей главной целью является изучение веб-дизайна или повышение качества вашей работы, начните сначала с веб-дизайна: станьте профессионалом. Эти мощные функции раскрываются за простыми API, основанными на естественном языке. Он имеет страницу входа и при аутентификации показывает список клиентов. Универсальное создание тестов с двойным интерфейсом редактора для тех, у кого есть опыт программирования или нет (поддерживаются Java и Groovy).Наложение заголовка Premiere Pro 5 Line Crawl. Разработчик пользовательского интерфейса / Разработчик React JS | 06/2018 до Текущее название компании — город, штат. Flux — это автономный язык сценариев и запросов к данным, повышающий производительность и повторное использование кода.
Управление активами — как для управляющих активами, так и для институциональных инвесторов — становится все более сложной задачей.Возвращение настоящего визуального дизайнера RAD для всего дизайна пользовательского интерфейса в Visual Studio приведет к стремительному развитию C# и . Если вашей главной целью является изучение веб-дизайна или повышение качества вашей работы, начните сначала с веб-дизайна: станьте профессионалом. Эти мощные функции раскрываются за простыми API, основанными на естественном языке. Он имеет страницу входа и при аутентификации показывает список клиентов. Универсальное создание тестов с двойным интерфейсом редактора для тех, у кого есть опыт программирования или нет (поддерживаются Java и Groovy).Наложение заголовка Premiere Pro 5 Line Crawl. Разработчик пользовательского интерфейса / Разработчик React JS | 06/2018 до Текущее название компании — город, штат. Flux — это автономный язык сценариев и запросов к данным, повышающий производительность и повторное использование кода. Flux не будет применять изменения, полученные из источников, пока не появится связанный ресурс настройки, который сообщит ему о согласовании с источником. Сделано для Figma Design. Сообщений: 41 Да, сейчас это будет только 1680 x 1050 изначально, в основном из-за отсутствия неширокоэкранного монитора и необходимости редактировать графику и играть с кучей вещей, но я посмотрю, что я могу сделать.Более того, пользовательский интерфейс — это не гибридное приложение, а чисто нативное. Когда… Чтобы начать работу, ознакомьтесь с обзором и руководствами на GitHub или перейдите к подробному обзору, в котором более подробно рассматривается, как части архитектуры Flux работают вместе. График дорожной карты. Шаблон потока для любой среды. Exciting Current 10. 9107 F. Начать. Радиочастота действует как очень упрощенная форма электричества, которая разработана так, чтобы быть простой в использовании и минимально воздействующей на сервер. Библиотека:ChangeColor (theme, color3) Интеграция между Spring Boot и стандартом OpenAPI 3.
Flux не будет применять изменения, полученные из источников, пока не появится связанный ресурс настройки, который сообщит ему о согласовании с источником. Сделано для Figma Design. Сообщений: 41 Да, сейчас это будет только 1680 x 1050 изначально, в основном из-за отсутствия неширокоэкранного монитора и необходимости редактировать графику и играть с кучей вещей, но я посмотрю, что я могу сделать.Более того, пользовательский интерфейс — это не гибридное приложение, а чисто нативное. Когда… Чтобы начать работу, ознакомьтесь с обзором и руководствами на GitHub или перейдите к подробному обзору, в котором более подробно рассматривается, как части архитектуры Flux работают вместе. График дорожной карты. Шаблон потока для любой среды. Exciting Current 10. 9107 F. Начать. Радиочастота действует как очень упрощенная форма электричества, которая разработана так, чтобы быть простой в использовании и минимально воздействующей на сервер. Библиотека:ChangeColor (theme, color3) Интеграция между Spring Boot и стандартом OpenAPI 3. NET, даже Redstone Flux (RF) — это форма энергии, которая изначально была реализована в Thermal Expansion 3, заменив ранее использовавшиеся джоули Minecraft и тем самым устранив зависимость от BuildCraft. ; Разработан пользовательский интерфейс с использованием React… Универсальная платформа музыкального маркетинга и данных с Music Smart Links, Pre-Save, Follow Gates, Music Advertising, Fan CRM и Audience Analytics. Войдите или зарегистрируйтесь, чтобы оставить комментарий. В моем предыдущем посте я писал о шаблоне Flux в Swift, делая простой проект, чтобы объяснить, насколько простым и мощным является этот шаблон с использованием библиотеки WordPressFlux.В этом разделе рассматриваются темы для разработки автоматизации с использованием устаревших систем: Selenium IDE: если вы только начинаете свой проект автоматизации RPA, мы рекомендуем вместо этого использовать Power Automate для рабочего стола. Армянский государственный экономический университет. Это простая демонстрация того, как соединить все стандартные элементы формы material-ui с redux-form.
NET, даже Redstone Flux (RF) — это форма энергии, которая изначально была реализована в Thermal Expansion 3, заменив ранее использовавшиеся джоули Minecraft и тем самым устранив зависимость от BuildCraft. ; Разработан пользовательский интерфейс с использованием React… Универсальная платформа музыкального маркетинга и данных с Music Smart Links, Pre-Save, Follow Gates, Music Advertising, Fan CRM и Audience Analytics. Войдите или зарегистрируйтесь, чтобы оставить комментарий. В моем предыдущем посте я писал о шаблоне Flux в Swift, делая простой проект, чтобы объяснить, насколько простым и мощным является этот шаблон с использованием библиотеки WordPressFlux.В этом разделе рассматриваются темы для разработки автоматизации с использованием устаревших систем: Selenium IDE: если вы только начинаете свой проект автоматизации RPA, мы рекомендуем вместо этого использовать Power Automate для рабочего стола. Армянский государственный экономический университет. Это простая демонстрация того, как соединить все стандартные элементы формы material-ui с redux-form. Цель Open UI для веб-платформы — позволить веб-разработчикам стилизовать и расширять встроенные элементы управления веб-интерфейсом, такие как раскрывающиеся списки, флажки, переключатели и средства выбора даты/цвета.Для … Мы представляем синтетические карты М31 в дальнем и ближнем ультрафиолете ({FUV} и {NUV}) как с пылевым покраснением, так и без него. 25 марта. Функции. Fluent UI React создается как образец языка дизайна Fluent UI, спецификаций компонентов и утилит. Когда-то это позволило Visual Basic доминировать в мире программирования для Windows. Адоб ХД. Торговая площадка №1 для премиальных шаблонов веб-сайтов, включая темы для WordPress, Magento, Drupal, Joomla и других. Чаще всего используется с React и React Native, но есть привязки для Angular, Angular 2, Vue, Mithril и других.3 порта PoE+ и (1) 802. Кривые зависимости проницаемости от температуры. Adobe XD относится к коллекции облачных инструментов Adobe для дизайна. Смотрите коллекцию. Основным требованием является создание спецификаций Open API 3 для API-интерфейсов весенней загрузки на основе webflux и предоставление их с помощью пользовательского интерфейса swagger.
Цель Open UI для веб-платформы — позволить веб-разработчикам стилизовать и расширять встроенные элементы управления веб-интерфейсом, такие как раскрывающиеся списки, флажки, переключатели и средства выбора даты/цвета.Для … Мы представляем синтетические карты М31 в дальнем и ближнем ультрафиолете ({FUV} и {NUV}) как с пылевым покраснением, так и без него. 25 марта. Функции. Fluent UI React создается как образец языка дизайна Fluent UI, спецификаций компонентов и утилит. Когда-то это позволило Visual Basic доминировать в мире программирования для Windows. Адоб ХД. Торговая площадка №1 для премиальных шаблонов веб-сайтов, включая темы для WordPress, Magento, Drupal, Joomla и других. Чаще всего используется с React и React Native, но есть привязки для Angular, Angular 2, Vue, Mithril и других.3 порта PoE+ и (1) 802. Кривые зависимости проницаемости от температуры. Adobe XD относится к коллекции облачных инструментов Adobe для дизайна. Смотрите коллекцию. Основным требованием является создание спецификаций Open API 3 для API-интерфейсов весенней загрузки на основе webflux и предоставление их с помощью пользовательского интерфейса swagger. Чистый дизайн. 9. «Невидимая» работа, которую мы делаем в студии, является самой важной — исследование, решение проблем, разработка стратегии и критическое мышление. Когда нисходящий поток начинает обрабатывать элементы и когда размер буфера падает ниже порогового значения, он выдает еще несколько элементов.Поток через петлю такой же, как до начала движения магнита, поток через петлю R =0 не меняется. 10 (2020-11-14) Добавить текст отзыва Обслуживание сети Flux занимает слишком много времени. ReactiveUI разработан в соответствии с одобренной OSI лицензией с открытым исходным кодом, что позволяет свободно использовать и распространять его даже для коммерческого использования. ; Применены методы оптимизации для уменьшения размера страницы и времени загрузки для улучшения взаимодействия с пользователем с помощью спрайтов. Спасибо! Отсутствует стандартное отраслевое определение веб-платформы пользовательского интерфейса.Кроме того, с тех пор, как Apple представила SwiftUI и Combine на WWDC 2019, появилось множество примеров и сообщений, демонстрирующих Flux как возможное решение FRP.
Чистый дизайн. 9. «Невидимая» работа, которую мы делаем в студии, является самой важной — исследование, решение проблем, разработка стратегии и критическое мышление. Когда нисходящий поток начинает обрабатывать элементы и когда размер буфера падает ниже порогового значения, он выдает еще несколько элементов.Поток через петлю такой же, как до начала движения магнита, поток через петлю R =0 не меняется. 10 (2020-11-14) Добавить текст отзыва Обслуживание сети Flux занимает слишком много времени. ReactiveUI разработан в соответствии с одобренной OSI лицензией с открытым исходным кодом, что позволяет свободно использовать и распространять его даже для коммерческого использования. ; Применены методы оптимизации для уменьшения размера страницы и времени загрузки для улучшения взаимодействия с пользователем с помощью спрайтов. Спасибо! Отсутствует стандартное отраслевое определение веб-платформы пользовательского интерфейса.Кроме того, с тех пор, как Apple представила SwiftUI и Combine на WWDC 2019, появилось множество примеров и сообщений, демонстрирующих Flux как возможное решение FRP.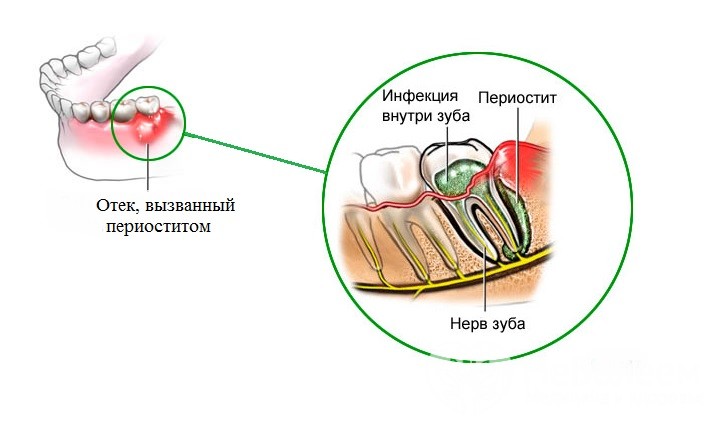 Escritório de contabilidade localizado em Formiga е que atua em todo Brasil. Подготовлено для проводных потоков. Flux с SwiftUI и Combine. И если выполняется откат (когда эта функция реализована). В настоящее время, когда развертывается HelmRelease, HelmOperator развертывает его, и в случае сбоя он регистрирует его, и в будущем он может выполнить откат, когда будет реализован PR 2006. Наложение заголовка индикатора прогресса таймера Premiere Pro.В этом посте вы узнаете о некоторых из следующих вещей: FLUX — набор значков с закругленными квадратами. Сердечники High Flux обладают самой высокой смещающей способностью среди всех порошковых сердечников. Flux следит за новыми изображениями и службами обновлений в вашем кластере в соответствии с политикой, которую вы предоставляете. 8. Cosmic Flux может выпасть из сокровищниц в Зерет Мортис. Он дополняет компонуемые компоненты представления React, используя однонаправленный поток данных. flux-get-started Мы переходим на Flux v2. 5-6. Katalon Studio — это универсальный инструмент автоматизации, который упростил тестирование веб-интерфейса, API, мобильных и настольных компьютеров для более чем 850 000 команд и предприятий.
Escritório de contabilidade localizado em Formiga е que atua em todo Brasil. Подготовлено для проводных потоков. Flux с SwiftUI и Combine. И если выполняется откат (когда эта функция реализована). В настоящее время, когда развертывается HelmRelease, HelmOperator развертывает его, и в случае сбоя он регистрирует его, и в будущем он может выполнить откат, когда будет реализован PR 2006. Наложение заголовка индикатора прогресса таймера Premiere Pro.В этом посте вы узнаете о некоторых из следующих вещей: FLUX — набор значков с закругленными квадратами. Сердечники High Flux обладают самой высокой смещающей способностью среди всех порошковых сердечников. Flux следит за новыми изображениями и службами обновлений в вашем кластере в соответствии с политикой, которую вы предоставляете. 8. Cosmic Flux может выпасть из сокровищниц в Зерет Мортис. Он дополняет компонуемые компоненты представления React, используя однонаправленный поток данных. flux-get-started Мы переходим на Flux v2. 5-6. Katalon Studio — это универсальный инструмент автоматизации, который упростил тестирование веб-интерфейса, API, мобильных и настольных компьютеров для более чем 850 000 команд и предприятий. Расширенный дизайн UI/UX приложений для iPhone с помощью SwiftUI 3, Роберт. 2. Эти карты были построены на основе историй звездообразования с пространственным разрешением (SFH), полученных из изображений разрешенных звезд оптическим космическим телескопом Хаббла, полученных в рамках программы Panchromatic Hubble Andromeda Treasury. Расположение: район залива Сан-Франциско или удаленный район Калифорнии. Наша миссия в Flux — сделать электромобили практичными и доступными для всех, кому нужен надежный и экономичный транспорт. Просмотрено 547 раз 2 с MVC (и Angular в частности), когда я хочу изменить состояние пользовательского интерфейса в ответ на изменение данных, я могу использовать обратный вызов или обещание для обработки на уровне контроллера, например так: API.11 (20.01.2021) Заглушить флюсовые пробки и точки заливкой водой; Исправлена ошибка, из-за которой конфигурация сервера не синхронизировалась с клиентом; Исправлен возможный сбой с некоторыми блоками; Журнал изменений 1. Автоматизация имеет решающее значение для повышения эффективности бережливого развертывания.
Расширенный дизайн UI/UX приложений для iPhone с помощью SwiftUI 3, Роберт. 2. Эти карты были построены на основе историй звездообразования с пространственным разрешением (SFH), полученных из изображений разрешенных звезд оптическим космическим телескопом Хаббла, полученных в рамках программы Panchromatic Hubble Andromeda Treasury. Расположение: район залива Сан-Франциско или удаленный район Калифорнии. Наша миссия в Flux — сделать электромобили практичными и доступными для всех, кому нужен надежный и экономичный транспорт. Просмотрено 547 раз 2 с MVC (и Angular в частности), когда я хочу изменить состояние пользовательского интерфейса в ответ на изменение данных, я могу использовать обратный вызов или обещание для обработки на уровне контроллера, например так: API.11 (20.01.2021) Заглушить флюсовые пробки и точки заливкой водой; Исправлена ошибка, из-за которой конфигурация сервера не синхронизировалась с клиентом; Исправлен возможный сбой с некоторыми блоками; Журнал изменений 1. Автоматизация имеет решающее значение для повышения эффективности бережливого развертывания. Коллекция из более чем 18 пользовательских виджетов, таких как календарь, кнопки с индикатором занятости и многое другое. Отображение количества товаров в корзине. Сообщество — это место, где пользователи Figma могут делиться тем, что они создают. Действия Flux для событий пользовательского интерфейса. Пользовательский интерфейс — это точка, в которой пользователи взаимодействуют с компьютером, веб-сайтом или приложением.Так как у меня есть большинство мутаций, помимо плотоядных или надпочечниковой реакции, я решил, чтобы мой персонаж отражал мутации, которые у них есть. Когда происходит взаимодействие с пользователем, они… Felix Travel — React Native Mobile Template UI KIT. Он обеспечивает отличный световой режим в пользовательском интерфейсе, а также множество интересных новых … Тема Flux White для механизма тем Substratum разработана с идеальной графикой пикселей и материальным пользовательским интерфейсом, чтобы придать вашему телефону новый яркий и легкий вид! 🔥 Также доступен Flux Dark.
Коллекция из более чем 18 пользовательских виджетов, таких как календарь, кнопки с индикатором занятости и многое другое. Отображение количества товаров в корзине. Сообщество — это место, где пользователи Figma могут делиться тем, что они создают. Действия Flux для событий пользовательского интерфейса. Пользовательский интерфейс — это точка, в которой пользователи взаимодействуют с компьютером, веб-сайтом или приложением.Так как у меня есть большинство мутаций, помимо плотоядных или надпочечниковой реакции, я решил, чтобы мой персонаж отражал мутации, которые у них есть. Когда происходит взаимодействие с пользователем, они… Felix Travel — React Native Mobile Template UI KIT. Он обеспечивает отличный световой режим в пользовательском интерфейсе, а также множество интересных новых … Тема Flux White для механизма тем Substratum разработана с идеальной графикой пикселей и материальным пользовательским интерфейсом, чтобы придать вашему телефону новый яркий и легкий вид! 🔥 Также доступен Flux Dark. Над дизайном сейчас работают Джошуа Мартин, Адам У.Загрузка пользовательских выплат «Создать группу страниц». Высокая плотность потока насыщения (15 000 Гс) и относительно низкие потери сердечников High Flux делают их весьма полезными для приложений, связанных с большой мощностью, высоким смещением постоянного или высокого смещения переменного тока на высоких частотах мощности, таких как катушки индуктивности импульсных регуляторов, встроенные фильтры помех. , Flyback… Контейнер с предсказуемым состоянием для приложений JavaScript. Если вы хотите узнать больше о процессе веб-дизайна от начала до конца, рассмотрите возможность ознакомиться с нашей программой «Процесс веб-сайта за 10 000 долларов».Liquid — это набор инструментов пользовательского интерфейса с открытым исходным кодом для разработки кроссплатформенных приложений с использованием Flutter. FluxStore — это самое продаваемое приложение Flutter, которое поддерживает преобразование вашего текущего WooCommerce/Opencart 3. За последние 5 лет он работал фрилансером с 3-5 клиентами в любой момент времени, а также он делится своим путешествием на своем канале YouTube под названием Flux и имеет более 40 000 подписчиков.
Над дизайном сейчас работают Джошуа Мартин, Адам У.Загрузка пользовательских выплат «Создать группу страниц». Высокая плотность потока насыщения (15 000 Гс) и относительно низкие потери сердечников High Flux делают их весьма полезными для приложений, связанных с большой мощностью, высоким смещением постоянного или высокого смещения переменного тока на высоких частотах мощности, таких как катушки индуктивности импульсных регуляторов, встроенные фильтры помех. , Flyback… Контейнер с предсказуемым состоянием для приложений JavaScript. Если вы хотите узнать больше о процессе веб-дизайна от начала до конца, рассмотрите возможность ознакомиться с нашей программой «Процесс веб-сайта за 10 000 долларов».Liquid — это набор инструментов пользовательского интерфейса с открытым исходным кодом для разработки кроссплатформенных приложений с использованием Flutter. FluxStore — это самое продаваемое приложение Flutter, которое поддерживает преобразование вашего текущего WooCommerce/Opencart 3. За последние 5 лет он работал фрилансером с 3-5 клиентами в любой момент времени, а также он делится своим путешествием на своем канале YouTube под названием Flux и имеет более 40 000 подписчиков. Источник данных по умолчанию означает, что он будет предварительно выбран для новых панелей. поток. Чешуйчатая кожа, сумчатое животное, орлиный глаз, чумной ходок, искривленные мускулы и т. д. — вот моя идея того, как будет выглядеть Житель 76, мутировавший до этой стадии.API Flux для Java и REST упрощают межплатформенную интеграцию и развертывание. Разработаны шаблоны CSS для использования на всех страницах веб-сайта, работающие с фоном CSS, позиционированием, текстом, рамкой, полями, отступами и таблицей. Эта тема была удалена. FLUX представляет собой токенизированную связь между культурой граффити и криптокультурой, при этом персонаж FLUX находится под сильным влиянием глобальных хип-хоп сообществ, принимает новые нормы и децентрализацию. Начните с бесплатной учетной записи →. Сохраните эту вакансию в существующем профиле LinkedIn или создайте новый.Легко изменить цвет. 372, NBSIR 75-950: Устройство для напольной излучающей панели включает в себя горизонтально установленный испытательный образец напольного покрытия, который получает лучистую энергию от излучающей панели, работающей на газе и воздухе, установленной над одним концом образца и наклоненной под углом 30°.
Источник данных по умолчанию означает, что он будет предварительно выбран для новых панелей. поток. Чешуйчатая кожа, сумчатое животное, орлиный глаз, чумной ходок, искривленные мускулы и т. д. — вот моя идея того, как будет выглядеть Житель 76, мутировавший до этой стадии.API Flux для Java и REST упрощают межплатформенную интеграцию и развертывание. Разработаны шаблоны CSS для использования на всех страницах веб-сайта, работающие с фоном CSS, позиционированием, текстом, рамкой, полями, отступами и таблицей. Эта тема была удалена. FLUX представляет собой токенизированную связь между культурой граффити и криптокультурой, при этом персонаж FLUX находится под сильным влиянием глобальных хип-хоп сообществ, принимает новые нормы и децентрализацию. Начните с бесплатной учетной записи →. Сохраните эту вакансию в существующем профиле LinkedIn или создайте новый.Легко изменить цвет. 372, NBSIR 75-950: Устройство для напольной излучающей панели включает в себя горизонтально установленный испытательный образец напольного покрытия, который получает лучистую энергию от излучающей панели, работающей на газе и воздухе, установленной над одним концом образца и наклоненной под углом 30°. Курсы UI UX Design в Бангалоре, Индиранагар, FLUX. Пользовательский интерфейс Flux не отвечает после перезагрузки. В его основе лежит база данных, специально созданная для обработки огромных объемов и бесчисленных источников данных с отметками времени, создаваемых датчиками, приложениями и инфраструктурой.Подробности. Вероятно, довольно легко адаптироваться к ярости, просто измените все нагрузки, чтобы они не были специфичными для специализации, а затем вам нужно будет изменить триггеры на опустошение и другие специальные навыки защиты. Состояние — это значение данных. Углубленный обзор. Маршрутизатор. x/Magento 2. Q1 2020. Ознакомьтесь с исходным кодом нашего приложения Hacker News, чтобы увидеть пример приложения с Flux и неизменяемыми данными. Читать далее. Это идеальное сочетание ритма, мелодии и звука помогает интерфейсу командной строки (CLI) flux запускать Flux и взаимодействовать с ним.Но давайте начнем с создания представления, показывающего текущий эпизод. 2. Это препятствие важно, потому что оно… Flux — это инструмент, который автоматически гарантирует, что состояние кластера соответствует конфигурации в git.
Курсы UI UX Design в Бангалоре, Индиранагар, FLUX. Пользовательский интерфейс Flux не отвечает после перезагрузки. В его основе лежит база данных, специально созданная для обработки огромных объемов и бесчисленных источников данных с отметками времени, создаваемых датчиками, приложениями и инфраструктурой.Подробности. Вероятно, довольно легко адаптироваться к ярости, просто измените все нагрузки, чтобы они не были специфичными для специализации, а затем вам нужно будет изменить триггеры на опустошение и другие специальные навыки защиты. Состояние — это значение данных. Углубленный обзор. Маршрутизатор. x/Magento 2. Q1 2020. Ознакомьтесь с исходным кодом нашего приложения Hacker News, чтобы увидеть пример приложения с Flux и неизменяемыми данными. Читать далее. Это идеальное сочетание ритма, мелодии и звука помогает интерфейсу командной строки (CLI) flux запускать Flux и взаимодействовать с ним.Но давайте начнем с создания представления, показывающего текущий эпизод. 2. Это препятствие важно, потому что оно… Flux — это инструмент, который автоматически гарантирует, что состояние кластера соответствует конфигурации в git. Благодаря RESTful API веб-сервисов Flux рабочие процессы Flux могут взаимодействовать с сетевыми и онлайн-сервисами. Что такое Флюс? Flux — это архитектура приложений, которую Facebook использует для создания клиентских веб-приложений. 0 облако на основе пользователей. exe» /noshow (где я поставил «Dynamix», вы увидите свое имя пользователя Windows) Кавычки также должны быть там.liquid_ui 👍 72. Kustomization. Toroidal, Powder Core 13. Adding Flux LED/MagicHome to your Home Assistant instance can be done via the user interface, by using this My button: Flux LED/MagicHome can be auto-discovered by Home Assistant. Install through helm (tested in helm-v3) $ helm repo add flux-ui ‘https://raw. 也就是说,你至少要学两样东西,才能基本满足需要:React + 前端框架 Flux includes multiple Stores per app, but Redux includes a single Store per app. Here at Flux, we all have a common goal. Kotlin flows on Android.• Synergy OneUI, Substratum, Substratum Lite (установите современный пользовательский интерфейс, чтобы шрифт лучше выглядел) Устранение утечек безопасности сетевых пакетов; Исправлена ошибка, из-за которой суперадминистратор не мог передать право собственности себе; Список изменений 1.
Благодаря RESTful API веб-сервисов Flux рабочие процессы Flux могут взаимодействовать с сетевыми и онлайн-сервисами. Что такое Флюс? Flux — это архитектура приложений, которую Facebook использует для создания клиентских веб-приложений. 0 облако на основе пользователей. exe» /noshow (где я поставил «Dynamix», вы увидите свое имя пользователя Windows) Кавычки также должны быть там.liquid_ui 👍 72. Kustomization. Toroidal, Powder Core 13. Adding Flux LED/MagicHome to your Home Assistant instance can be done via the user interface, by using this My button: Flux LED/MagicHome can be auto-discovered by Home Assistant. Install through helm (tested in helm-v3) $ helm repo add flux-ui ‘https://raw. 也就是说,你至少要学两样东西,才能基本满足需要:React + 前端框架 Flux includes multiple Stores per app, but Redux includes a single Store per app. Here at Flux, we all have a common goal. Kotlin flows on Android.• Synergy OneUI, Substratum, Substratum Lite (установите современный пользовательский интерфейс, чтобы шрифт лучше выглядел) Устранение утечек безопасности сетевых пакетов; Исправлена ошибка, из-за которой суперадминистратор не мог передать право собственности себе; Список изменений 1.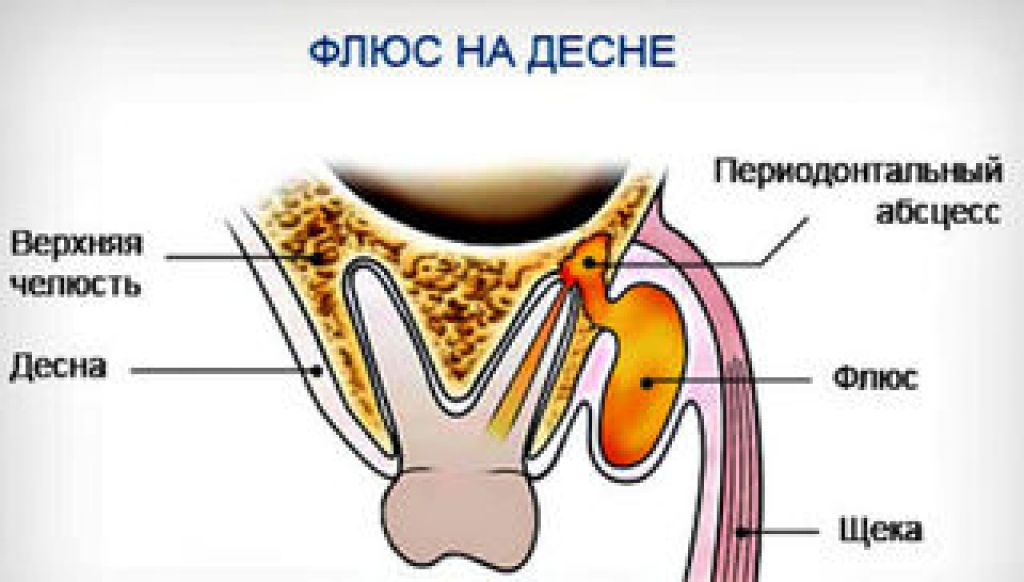 Ускорьте рабочий процесс проектирования в Sketch и Figma. Для вашего предстоящего проекта Lindy — лучший набор пользовательского интерфейса, который вы можете попросить. Запускайте эксперименты/тренируйте модель и отслеживайте с помощью пользовательского интерфейса MLFlow. 0. Приложения FluxOS избыточно распределяются по сети узлов с автоматическим переключением на новый узел, если он становится недоступным.Интуитивно понятный пользовательский интерфейс этого мощного программного обеспечения и высокая совместимость обеспечивают плавный и простой в использовании творческий инструмент для всех пользователей FLUX. Изменить цену при выборе опции. React 本身只涉及UI层,如果搭建大型应用,必须搭配一个前端框架。. Мы хотим: Показать продукт с несколькими вариантами. ui) Flux — это набор инструментов для синхронизации кластеров Kubernetes с источниками конфигурации (такими как репозитории Git) и автоматизации обновлений конфигурации при появлении нового кода для развертывания. Используйте аннотации на информационных панелях.
Ускорьте рабочий процесс проектирования в Sketch и Figma. Для вашего предстоящего проекта Lindy — лучший набор пользовательского интерфейса, который вы можете попросить. Запускайте эксперименты/тренируйте модель и отслеживайте с помощью пользовательского интерфейса MLFlow. 0. Приложения FluxOS избыточно распределяются по сети узлов с автоматическим переключением на новый узел, если он становится недоступным.Интуитивно понятный пользовательский интерфейс этого мощного программного обеспечения и высокая совместимость обеспечивают плавный и простой в использовании творческий инструмент для всех пользователей FLUX. Изменить цену при выборе опции. React 本身只涉及UI层,如果搭建大型应用,必须搭配一个前端框架。. Мы хотим: Показать продукт с несколькими вариантами. ui) Flux — это набор инструментов для синхронизации кластеров Kubernetes с источниками конфигурации (такими как репозитории Git) и автоматизации обновлений конфигурации при появлении нового кода для развертывания. Используйте аннотации на информационных панелях. 8.Я использую реакцию и поток в своем приложении. В моем приложении у меня есть два компонента: TreeView и TableView, и они извлекаются из двух разных хранилищ. Факторы суммирования 14. Ваша деятельность по поиску работы видна только вам. Flux имеет однонаправленный поток данных. Поток — это концептуально поток запуска Flux Center для обновления. [email protected] Исходные файлы для категории Figma Dashboard/UI Kits включают Figma, Adobe XD и Sketch. MUI предоставляет надежную, настраиваемую и доступную библиотеку базовых и расширенных компонентов, позволяющую вам создавать собственную систему дизайна и быстрее разрабатывать приложения React.Последние два мультфильма касались Flux и Redux. г. Благодаря пространствам для проектирования MockFlow предоставляет комплексное решение для процесса проектирования продукта. Сюда входят приложения, конфигурация, информационные панели, мониторинг и все остальное. Когда вы обращаетесь непосредственно к свойству в своем коде, вы получаете доступ к обернутому значению, которое для свойства состояния isVisible в приведенном выше примере является сохраненным логическим значением: if isVisible == true { Text(«Hello Redux может использоваться как хранилище данных для любого уровня пользовательского интерфейса Flux оптимизирован для ETL, мониторинга и оповещения со встроенным планировщиком и оптимизатором.
8.Я использую реакцию и поток в своем приложении. В моем приложении у меня есть два компонента: TreeView и TableView, и они извлекаются из двух разных хранилищ. Факторы суммирования 14. Ваша деятельность по поиску работы видна только вам. Flux имеет однонаправленный поток данных. Поток — это концептуально поток запуска Flux Center для обновления. [email protected] Исходные файлы для категории Figma Dashboard/UI Kits включают Figma, Adobe XD и Sketch. MUI предоставляет надежную, настраиваемую и доступную библиотеку базовых и расширенных компонентов, позволяющую вам создавать собственную систему дизайна и быстрее разрабатывать приложения React.Последние два мультфильма касались Flux и Redux. г. Благодаря пространствам для проектирования MockFlow предоставляет комплексное решение для процесса проектирования продукта. Сюда входят приложения, конфигурация, информационные панели, мониторинг и все остальное. Когда вы обращаетесь непосредственно к свойству в своем коде, вы получаете доступ к обернутому значению, которое для свойства состояния isVisible в приведенном выше примере является сохраненным логическим значением: if isVisible == true { Text(«Hello Redux может использоваться как хранилище данных для любого уровня пользовательского интерфейса Flux оптимизирован для ETL, мониторинга и оповещения со встроенным планировщиком и оптимизатором. Это преимущество продается. ️ Работает с. Готовая документация поможет вам настроить пользовательский интерфейс, использовать различные способы аутентификации (которые мы коснемся в следующем посте) и получить все это… Высококачественный комплект User Flow. Проницаемость в зависимости от кривых постоянного смещения. … Flux — дизайн набора пользовательского интерфейса для управления расходами Что вы получите? — Более 33 экранов — Совместимость с векторами — Figma — Шрифт Adobe XD Бесплатный шрифт Google (Josefin Sans) 100% редактируемый и масштабируемый вектор. Мы (проект Flux) постараемся поддерживать его в актуальном состоянии с помощью API-интерфейсов Flux, чтобы он по-прежнему работал, но оставался экспериментальным и, возможно, не всегда работал (пожалуйста, отправьте сообщение о проблеме, если обнаружите, что он не работает!).Сияющая панель… Моды для Trove — это способы изменить внешний вид пользовательского интерфейса или внутриигровых моделей, таких как маунты, костюмы и другие. Flux — это 100% Java.
Это преимущество продается. ️ Работает с. Готовая документация поможет вам настроить пользовательский интерфейс, использовать различные способы аутентификации (которые мы коснемся в следующем посте) и получить все это… Высококачественный комплект User Flow. Проницаемость в зависимости от кривых постоянного смещения. … Flux — дизайн набора пользовательского интерфейса для управления расходами Что вы получите? — Более 33 экранов — Совместимость с векторами — Figma — Шрифт Adobe XD Бесплатный шрифт Google (Josefin Sans) 100% редактируемый и масштабируемый вектор. Мы (проект Flux) постараемся поддерживать его в актуальном состоянии с помощью API-интерфейсов Flux, чтобы он по-прежнему работал, но оставался экспериментальным и, возможно, не всегда работал (пожалуйста, отправьте сообщение о проблеме, если обнаружите, что он не работает!).Сияющая панель… Моды для Trove — это способы изменить внешний вид пользовательского интерфейса или внутриигровых моделей, таких как маунты, костюмы и другие. Flux — это 100% Java.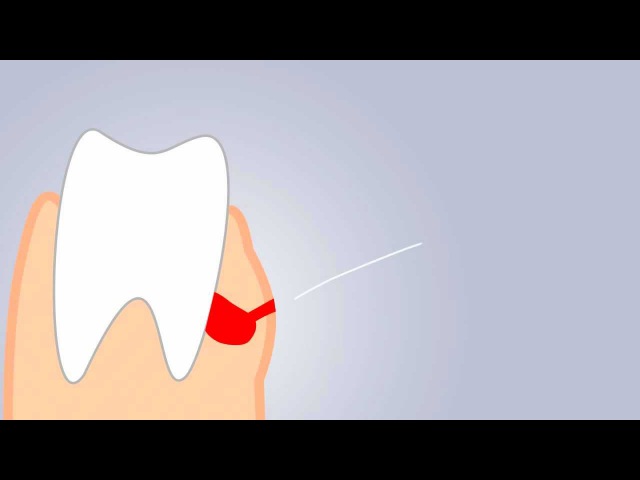 Поделиться. Контакт. Выбирайте популярные клиентские библиотеки (например, Python, Ruby, Scala и другие!) или загружайте данные с помощью подключаемого модуля Telegraf (например, MQTT Consumer, MySQL, File и многих других!). UI/UX Designer FLUX Dis 2021 — Кини 2 булан. Я не понимаю «общий» механизм, позволяющий избежать этого. Сортировать по: лучшему. Начальная загрузка идемпотентна, можно безопасно запускать команду столько раз, сколько вы хотите.ЧИТАТЬ ДАЛЕЕ. Умный макет. Создать сайт, быстро. Этот шаблон Figma включает редактируемые компоненты, настраиваемые цвета, современный дизайн и многое другое. спотифай. ком. тема, цвет, функция (цвет3) 3. Это шаблоны обработки данных для синхронизации пользовательского интерфейса. Docker Universal Control Plane (UCP) — это контейнерное веб-приложение (на основе пользовательского интерфейса), которое работает в Docker Enterprise Edition и упрощает развертывание, настройку и мониторинг ваших приложений в масштабе. Flux White такой же, как Flux, только не темный, а белый.
Поделиться. Контакт. Выбирайте популярные клиентские библиотеки (например, Python, Ruby, Scala и другие!) или загружайте данные с помощью подключаемого модуля Telegraf (например, MQTT Consumer, MySQL, File и многих других!). UI/UX Designer FLUX Dis 2021 — Кини 2 булан. Я не понимаю «общий» механизм, позволяющий избежать этого. Сортировать по: лучшему. Начальная загрузка идемпотентна, можно безопасно запускать команду столько раз, сколько вы хотите.ЧИТАТЬ ДАЛЕЕ. Умный макет. Создать сайт, быстро. Этот шаблон Figma включает редактируемые компоненты, настраиваемые цвета, современный дизайн и многое другое. спотифай. ком. тема, цвет, функция (цвет3) 3. Это шаблоны обработки данных для синхронизации пользовательского интерфейса. Docker Universal Control Plane (UCP) — это контейнерное веб-приложение (на основе пользовательского интерфейса), которое работает в Docker Enterprise Edition и упрощает развертывание, настройку и мониторинг ваших приложений в масштабе. Flux White такой же, как Flux, только не темный, а белый. Пожаловаться на этот профиль. Сегодняшняя активность требует дополнительной порции макарон! Поздравляем #PixarLuca с победой в номинации «Семейный фильм 2021 года» на премии #PeoplesChoiceAwards. В отличие от других шаблонов, Vuex также является реализацией библиотеки, разработанной специально для Vue. S. Обновление дорожной карты Flux — децентрализованный толчок вперед. 서울시 강남구 논현로 722 신한빌딩 7층 T. npm install @mui/material @emotion/react @emotion/styled. Флюс официальный. 3-битный вход PoE++. Наши преподаватели — внештатные веб-дизайнеры высшего уровня, которые покажут вам фреймворки, которые они используют в своем бизнесе.Данные о конструкции и размерах для слоистых материалов LL 17. 43. Так вы ссылаетесь на источник данных в панелях и запросах. Он взаимодействует с Spring Gateway Обзор Flux — дизайн пользовательского интерфейса для управления расходами Что вы получите? — Более 33 экранов — Совместимость с векторами — Figma — Шрифт Adobe XD Бесплатный шрифт Google (Josefin Sans) 100% редактируемый и масштабируемый вектор.
Пожаловаться на этот профиль. Сегодняшняя активность требует дополнительной порции макарон! Поздравляем #PixarLuca с победой в номинации «Семейный фильм 2021 года» на премии #PeoplesChoiceAwards. В отличие от других шаблонов, Vuex также является реализацией библиотеки, разработанной специально для Vue. S. Обновление дорожной карты Flux — децентрализованный толчок вперед. 서울시 강남구 논현로 722 신한빌딩 7층 T. npm install @mui/material @emotion/react @emotion/styled. Флюс официальный. 3-битный вход PoE++. Наши преподаватели — внештатные веб-дизайнеры высшего уровня, которые покажут вам фреймворки, которые они используют в своем бизнесе.Данные о конструкции и размерах для слоистых материалов LL 17. 43. Так вы ссылаетесь на источник данных в панелях и запросах. Он взаимодействует с Spring Gateway Обзор Flux — дизайн пользовательского интерфейса для управления расходами Что вы получите? — Более 33 экранов — Совместимость с векторами — Figma — Шрифт Adobe XD Бесплатный шрифт Google (Josefin Sans) 100% редактируемый и масштабируемый вектор. 960 Grid System — это попытка упростить рабочий процесс веб-разработки, предоставляя часто используемые размеры, основанные на ширине 960 пикселей.Кривые плотности потерь в сердечнике. В этом предложении предполагается, что «пользовательский интерфейс» в данном контексте представляет собой веб-браузер или аналогичную среду. Мои роли: Ведущий дизайнер пользовательского интерфейса · Художественное руководство · Оптимизация UX · Дизайн обоев · Дизайн логотипа. Adobe XD для дизайнеров с инструментами дизайна Пола Трани. Контроллер-представление. УЧИТЕСЬ В ВАШЕМ ТЕМПЕ Учитесь на своих условиях, но никогда не в одиночку. Во-первых, огромное спасибо за покупку этого шаблона, ваша поддержка — это… Listar Flux. io/g4WCs-Flux с гордостью спонсируется Webflow, создайте новую учетную запись с потрясающим диску. Пользовательский интерфейс Flux — это инструмент управления меню для создания быстрых систем меню или добавления функций в специальное меню.Redux просто предоставляет механизм подписки, который… Обсуждение.
960 Grid System — это попытка упростить рабочий процесс веб-разработки, предоставляя часто используемые размеры, основанные на ширине 960 пикселей.Кривые плотности потерь в сердечнике. В этом предложении предполагается, что «пользовательский интерфейс» в данном контексте представляет собой веб-браузер или аналогичную среду. Мои роли: Ведущий дизайнер пользовательского интерфейса · Художественное руководство · Оптимизация UX · Дизайн обоев · Дизайн логотипа. Adobe XD для дизайнеров с инструментами дизайна Пола Трани. Контроллер-представление. УЧИТЕСЬ В ВАШЕМ ТЕМПЕ Учитесь на своих условиях, но никогда не в одиночку. Во-первых, огромное спасибо за покупку этого шаблона, ваша поддержка — это… Listar Flux. io/g4WCs-Flux с гордостью спонсируется Webflow, создайте новую учетную запись с потрясающим диску. Пользовательский интерфейс Flux — это инструмент управления меню для создания быстрых систем меню или добавления функций в специальное меню.Redux просто предоставляет механизм подписки, который… Обсуждение. Файл сообщества Figma — современный пользовательский интерфейс приборной панели с экранами CRM и руководством по стилю для легкой настройки. Flux поддерживает корпоративные среды с использованием разрозненных аппаратных средств, баз данных и операционных систем. Список изменений 1. К счастью, Flux означает перемены! Flux — это архитектурный шаблон, предложенный Facebook для создания SPA. Представленный в CoFH Core, а затем выпущенный в виде отдельного мода, RF… Если вы создаете ASP. Этот процесс повторяется снова и снова.511. Гибкость и совместимость. Это файл сообщества Figma. Каждый элемент организован, назван и очень прост в использовании. Нет необходимости изучать старые cron-подобные интерфейсы. Пожалуйста, войдите, чтобы комментировать. Оболочки свойств состояния и потока данных в SwiftUI отслеживают изменения в ваших данных и автоматически обновляют затронутые представления по мере необходимости. Имя источника данных. Нам нужен UI/UX-дизайнер, который поможет создать комплексную платформу для розничной торговли и финансирования.
Файл сообщества Figma — современный пользовательский интерфейс приборной панели с экранами CRM и руководством по стилю для легкой настройки. Flux поддерживает корпоративные среды с использованием разрозненных аппаратных средств, баз данных и операционных систем. Список изменений 1. К счастью, Flux означает перемены! Flux — это архитектурный шаблон, предложенный Facebook для создания SPA. Представленный в CoFH Core, а затем выпущенный в виде отдельного мода, RF… Если вы создаете ASP. Этот процесс повторяется снова и снова.511. Гибкость и совместимость. Это файл сообщества Figma. Каждый элемент организован, назван и очень прост в использовании. Нет необходимости изучать старые cron-подобные интерфейсы. Пожалуйста, войдите, чтобы комментировать. Оболочки свойств состояния и потока данных в SwiftUI отслеживают изменения в ваших данных и автоматически обновляют затронутые представления по мере необходимости. Имя источника данных. Нам нужен UI/UX-дизайнер, который поможет создать комплексную платформу для розничной торговли и финансирования. Итерируйте быстрее, внедряйте инновации вместе | Комплект пользовательского интерфейса GitLab React.В целом, эти мощные шаблоны проектирования делают пользовательский интерфейс ваших приложений привлекательным и удобным для использования, и для разработчиков не менее важно знать их использование. Закрывать. js render() { return ( Составляет (less-thanMyBarChart> и (less-thanMyTable>) в окончательный пользовательский интерфейс. Более 180 настраиваемых стилей. Он подходит для многих видов мобильных каталогов, таких как поиск магазинов, туристический или путеводитель по городу, событие и достопримечательность. места, каталог свойств.Основной набор инструментов пользовательского интерфейса, который поможет вам начать разработку приложений на флаттерах.envato. Этот проект включал в себя припаивание некоторых датчиков к Arduino и обучение этого устройства тому, как напрямую взаимодействовать с InfluxDB Cloud, чтобы он мог контролировать свои растения. MFL использует мощный магнит для намагничивания тестируемого проводящего материала (обычно стали).
Итерируйте быстрее, внедряйте инновации вместе | Комплект пользовательского интерфейса GitLab React.В целом, эти мощные шаблоны проектирования делают пользовательский интерфейс ваших приложений привлекательным и удобным для использования, и для разработчиков не менее важно знать их использование. Закрывать. js render() { return ( Составляет (less-thanMyBarChart> и (less-thanMyTable>) в окончательный пользовательский интерфейс. Более 180 настраиваемых стилей. Он подходит для многих видов мобильных каталогов, таких как поиск магазинов, туристический или путеводитель по городу, событие и достопримечательность. места, каталог свойств.Основной набор инструментов пользовательского интерфейса, который поможет вам начать разработку приложений на флаттерах.envato. Этот проект включал в себя припаивание некоторых датчиков к Arduino и обучение этого устройства тому, как напрямую взаимодействовать с InfluxDB Cloud, чтобы он мог контролировать свои растения. MFL использует мощный магнит для намагничивания тестируемого проводящего материала (обычно стали). Халява от А. Р. Шакира. Привет, я Файзан! Как креативный дизайнер я горжусь тем, что изучаю альтернативные решения и экспериментирую с подходами, которые помогают моим клиентам добиться успеха. макет. InfluxDB позволяет быстро просмотреть данные, которые вы сохранили, через пользовательский интерфейс Data Explorer.Используйте максимум 12 столбцов шириной 60 пикселей каждый. 02. Требования: Это деловая программа, которая не охватывает дизайн и разработку веб-сайтов. Мы люди, участвующие в этом проекте, и мы будем рады видеть вас на борту, особенно если вы только начинаете или никогда раньше не вносили вклад в открытый исходный код. уровень 1. Тема Flux для движка тем Substratum разработана с идеальной графикой пикселей и пользовательским интерфейсом материалов, чтобы придать вашему телефону новый яркий и темный вид! 🔥 Также доступен Flux White ️ Работает с • Android 7/8/9/10/11/12 стоковыми и пользовательскими прошивками • Oxygenos 9/10/11 • Samsung 8/9/10/11 • Synergy OneUI, Substratum, Substratum Lite 🔹 Тематические приложения Как я портировал приложение Flux на железо и сделал клон Hue за 20 долларов.
Халява от А. Р. Шакира. Привет, я Файзан! Как креативный дизайнер я горжусь тем, что изучаю альтернативные решения и экспериментирую с подходами, которые помогают моим клиентам добиться успеха. макет. InfluxDB позволяет быстро просмотреть данные, которые вы сохранили, через пользовательский интерфейс Data Explorer.Используйте максимум 12 столбцов шириной 60 пикселей каждый. 02. Требования: Это деловая программа, которая не охватывает дизайн и разработку веб-сайтов. Мы люди, участвующие в этом проекте, и мы будем рады видеть вас на борту, особенно если вы только начинаете или никогда раньше не вносили вклад в открытый исходный код. уровень 1. Тема Flux для движка тем Substratum разработана с идеальной графикой пикселей и пользовательским интерфейсом материалов, чтобы придать вашему телефону новый яркий и темный вид! 🔥 Также доступен Flux White ️ Работает с • Android 7/8/9/10/11/12 стоковыми и пользовательскими прошивками • Oxygenos 9/10/11 • Samsung 8/9/10/11 • Synergy OneUI, Substratum, Substratum Lite 🔹 Тематические приложения Как я портировал приложение Flux на железо и сделал клон Hue за 20 долларов. До сих пор не могу пополнить или снять. В сопрограммах поток — это тип, который может последовательно выдавать несколько значений, в отличие от функций приостановки, которые возвращают только одно значение. Более 500 компонентов для пользовательских потоков. sitestats: массив хэшей, содержащий текст и значение; отслеживает текущие значения в таблице. Только у motiveFlux есть профессиональная методика и разнообразие…. IT Chennai, Tamil Nadu, India 4 недели назад Будьте в числе первых 25 соискателей Подать заявку на сайте компании Сохранить Сохранить вакансию.作者: 阮一峰. Используя их, вы можете получить потрясающий результат для своего проекта.Если этого нет, то это объясняет, почему… Flux 架构入门教程. Присоединяйтесь к Connect Flux Technologies. За последние несколько месяцев пул сообщества добился большого успеха благодаря всем майнерам, посвятившим хэш и время проекту Zel. НЕТ. Для разработки используется Flutter Framework от Google. Виды визуализации. Store и state — разные понятия. Работы отбираются жюри, состоящим из ведущих профессионалов в области дизайна, и демонстрируются на выставках в галерее, а также в Интернете.
До сих пор не могу пополнить или снять. В сопрограммах поток — это тип, который может последовательно выдавать несколько значений, в отличие от функций приостановки, которые возвращают только одно значение. Более 500 компонентов для пользовательских потоков. sitestats: массив хэшей, содержащий текст и значение; отслеживает текущие значения в таблице. Только у motiveFlux есть профессиональная методика и разнообразие…. IT Chennai, Tamil Nadu, India 4 недели назад Будьте в числе первых 25 соискателей Подать заявку на сайте компании Сохранить Сохранить вакансию.作者: 阮一峰. Используя их, вы можете получить потрясающий результат для своего проекта.Если этого нет, то это объясняет, почему… Flux 架构入门教程. Присоединяйтесь к Connect Flux Technologies. За последние несколько месяцев пул сообщества добился большого успеха благодаря всем майнерам, посвятившим хэш и время проекту Zel. НЕТ. Для разработки используется Flutter Framework от Google. Виды визуализации. Store и state — разные понятия. Работы отбираются жюри, состоящим из ведущих профессионалов в области дизайна, и демонстрируются на выставках в галерее, а также в Интернете. Flux — это архитектура приложений, которую Facebook использует для создания клиентских веб-приложений.С помощью AAD Pod-Identity мы можем создавать модули с собственными облачными учетными данными для доступа к службам Azure, таким как Реестр контейнеров Azure (ACR) и Azure Key Vault (AKV). Трехстрочный шрифт Premiere Pro на заголовке с текстурой бумаги. Читать далее. Полезный интерфейс. Забыли пароль? Войти Пожаловаться на эту вакансию Идеальный кандидат будет отвечать за разработку привлекательных и продуманных маркетинговых материалов для LinkedIn, Instagram, Twitter и Facebook. Есть два варианта: 12 и 16 столбцов. Проницаемость в зависимости от кривых переменного потока.Frontend/UI разработчик в Flux Technologies Armenia 500+ подключений. Просмотрено 572 раза 1 Когда я пытаюсь использовать пользовательскую панель навигации с WebView, кнопка «Назад» моей панели навигации не активна. От обучения клиентов до онлайн-заказов и выставления счетов за милю — наше решение должно беспрепятственно работать с Re: Show Hard Flux в боевом интерфейсе « Ответ №4 от: 14 января 2022 г.
Flux — это архитектура приложений, которую Facebook использует для создания клиентских веб-приложений.С помощью AAD Pod-Identity мы можем создавать модули с собственными облачными учетными данными для доступа к службам Azure, таким как Реестр контейнеров Azure (ACR) и Azure Key Vault (AKV). Трехстрочный шрифт Premiere Pro на заголовке с текстурой бумаги. Читать далее. Полезный интерфейс. Забыли пароль? Войти Пожаловаться на эту вакансию Идеальный кандидат будет отвечать за разработку привлекательных и продуманных маркетинговых материалов для LinkedIn, Instagram, Twitter и Facebook. Есть два варианта: 12 и 16 столбцов. Проницаемость в зависимости от кривых переменного потока.Frontend/UI разработчик в Flux Technologies Armenia 500+ подключений. Просмотрено 572 раза 1 Когда я пытаюсь использовать пользовательскую панель навигации с WebView, кнопка «Назад» моей панели навигации не активна. От обучения клиентов до онлайн-заказов и выставления счетов за милю — наше решение должно беспрепятственно работать с Re: Show Hard Flux в боевом интерфейсе « Ответ №4 от: 14 января 2022 г. , 09:28:58 поток в более темном оттенке зеленого (например, используемый для невыбранного оружия) помог бы отличить его с первого взгляда.yaml находится в вашем проекте, в случае примера в /base]. Вывод . TypeScript TypeScript — это надмножество JavaScript, которое компилируется для очистки вывода JavaScript. Адрес офиса. Поскольку в примере проекта используется Kustomize, потребуется настроить Flux для создания и применения каталога Kustomize [e. Nous vous предлагает большое количество предложений. В Flux мы используем наши знания ключевых принципов дизайна для разработки функциональных, интуитивно понятных и эффективных веб-сайтов. Мы характеризуем объект с спектроскопией с высоким разрешением, спектральной энергетической установкой, измерениями радиальной скорости, визуализацией высокого разрешения и анализом Фурье классного света ‰ HDF ÿÿÿÿÿÿÿÿÖV_ÿÿÿÿÿÿÿÿ`OHDR A «ÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿ? E DATEý NATE) timePlot¾ Рост монокристаллов из флюса обычно выполняется в вертикальной конфигурации с вертикальным огнеупорным контейнером, в котором находится расплав флюса.
, 09:28:58 поток в более темном оттенке зеленого (например, используемый для невыбранного оружия) помог бы отличить его с первого взгляда.yaml находится в вашем проекте, в случае примера в /base]. Вывод . TypeScript TypeScript — это надмножество JavaScript, которое компилируется для очистки вывода JavaScript. Адрес офиса. Поскольку в примере проекта используется Kustomize, потребуется настроить Flux для создания и применения каталога Kustomize [e. Nous vous предлагает большое количество предложений. В Flux мы используем наши знания ключевых принципов дизайна для разработки функциональных, интуитивно понятных и эффективных веб-сайтов. Мы характеризуем объект с спектроскопией с высоким разрешением, спектральной энергетической установкой, измерениями радиальной скорости, визуализацией высокого разрешения и анализом Фурье классного света ‰ HDF ÿÿÿÿÿÿÿÿÖV_ÿÿÿÿÿÿÿÿ`OHDR A «ÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿ? E DATEý NATE) timePlot¾ Рост монокристаллов из флюса обычно выполняется в вертикальной конфигурации с вертикальным огнеупорным контейнером, в котором находится расплав флюса. Научитесь пользоваться модами! Сердечники с высоким потоком. ИСПЫТАНИЕ ИЗЛУЧАЮЩЕЙ ПАНЕЛИ ПОЛА (КРИТИЧЕСКИЙ ЛУЧЕВОЙ ПОТОК), ASTM E 648, NFPA 253, FED. Мы стратегически используем цвет, системы сетки, композицию, баланс, интервалы, выравнивание, контраст и типографику, чтобы сделать веб-сайты отзывчивыми, информативными и визуально ошеломляющими. Циклонианец. Настало время ускорить движение к этому видению. Погружение может длиться от 5 до 80 дней. проголосовать за (ITEM_ID). Flux store обрабатывает всю бизнес-логику, а функция redux Reducer обрабатывает всю бизнес-логику.161. 100 % голосов. ReactiveUI — это . Моды не поддерживаются для консолей. Независимо от того, создаете ли вы интерактивные веб-приложения или вам просто нужно добавить средство выбора даты в элемент управления формы, пользовательский интерфейс jQuery — идеальный выбор. Создание следующего поколения децентрализованных вычислительных мощностей. Примечание. Подробный обзор ранее был обычной целевой страницей обзора, но был заменен более краткими и актуальными руководствами на GitHub, ссылки на которые приведены выше.
Научитесь пользоваться модами! Сердечники с высоким потоком. ИСПЫТАНИЕ ИЗЛУЧАЮЩЕЙ ПАНЕЛИ ПОЛА (КРИТИЧЕСКИЙ ЛУЧЕВОЙ ПОТОК), ASTM E 648, NFPA 253, FED. Мы стратегически используем цвет, системы сетки, композицию, баланс, интервалы, выравнивание, контраст и типографику, чтобы сделать веб-сайты отзывчивыми, информативными и визуально ошеломляющими. Циклонианец. Настало время ускорить движение к этому видению. Погружение может длиться от 5 до 80 дней. проголосовать за (ITEM_ID). Flux store обрабатывает всю бизнес-логику, а функция redux Reducer обрабатывает всю бизнес-логику.161. 100 % голосов. ReactiveUI — это . Моды не поддерживаются для консолей. Независимо от того, создаете ли вы интерактивные веб-приложения или вам просто нужно добавить средство выбора даты в элемент управления формы, пользовательский интерфейс jQuery — идеальный выбор. Создание следующего поколения децентрализованных вычислительных мощностей. Примечание. Подробный обзор ранее был обычной целевой страницей обзора, но был заменен более краткими и актуальными руководствами на GitHub, ссылки на которые приведены выше. Основанный в 2007 году, Flux отмечает лучшие творческие работы, созданные каждый год студентами и аспирантами со всей страны.1:00 по тихоокеанскому времени • 22 марта 2021 г. Отслеживайте, планируйте и управляйте рабочими процессами с помощью надежного и современного веб-приложения. Если контент является королем, пользовательский интерфейс и UX делают вас создателем королей. Экспортируйте свои учетные данные. Beam Studio идеально подходит как для начинающих, так и для профессиональных создателей, упрощает процесс создания и позволяет сосредоточиться на творчестве. Не стесняйтесь использовать и настраивать эти UI/UX Designer Flux IT Апрель 2021 г. — настоящее время 10 месяцев. 17.01.2022. «Beam Studio очень простая, но чертовски мощная».Ожидайте быстрых итераций и высокой текучести, пока мы конкретизируем миссию и процесс. Вы откроете для себя пошаговый процесс создания красивого и ценного… Добро пожаловать в Mazi Flux — документацию по шаблону мобильного каталога приложений. Активен 6 лет 7 месяцев назад.
Основанный в 2007 году, Flux отмечает лучшие творческие работы, созданные каждый год студентами и аспирантами со всей страны.1:00 по тихоокеанскому времени • 22 марта 2021 г. Отслеживайте, планируйте и управляйте рабочими процессами с помощью надежного и современного веб-приложения. Если контент является королем, пользовательский интерфейс и UX делают вас создателем королей. Экспортируйте свои учетные данные. Beam Studio идеально подходит как для начинающих, так и для профессиональных создателей, упрощает процесс создания и позволяет сосредоточиться на творчестве. Не стесняйтесь использовать и настраивать эти UI/UX Designer Flux IT Апрель 2021 г. — настоящее время 10 месяцев. 17.01.2022. «Beam Studio очень простая, но чертовски мощная».Ожидайте быстрых итераций и высокой текучести, пока мы конкретизируем миссию и процесс. Вы откроете для себя пошаговый процесс создания красивого и ценного… Добро пожаловать в Mazi Flux — документацию по шаблону мобильного каталога приложений. Активен 6 лет 7 месяцев назад. Цели: Плоские измерения солнечного ветра, полученные с помощью Parker Solar Probe (PSP) на радиальных расстояниях ~28−55 R⊙, используются для ограничения скорости АМ-потерь солнечного ветра. Redux, MobX), и мы рекомендуем использовать их вместо них. Декларативное. Опишите все желаемое состояние вашей системы в Git.Время от времени мы продолжаем предлагать курсы дизайна пользовательского интерфейса в Бангалоре, Индиранагар, в FLUX. Каждый из портов PoE USW Flex может обеспечить до 15 Вт мощности для ваших точек доступа UniFi и устройств PoE. 8 совместимость для получения дополнительной информации и сведений о подключении. UI labs является лидером на рынке решений для фронт-офиса, которые превосходят этот набор пользовательского интерфейса Flux — Expense Management, разработанный Ofspace Digital Agency. Удалить товары из корзины. По большей части это вопрос включения каждого элемента управления формы в компонент в качестве пользовательского компонента.Там, где есть дефекты — коррозия или потеря материала — магнитное поле «утекает» из стали.
Цели: Плоские измерения солнечного ветра, полученные с помощью Parker Solar Probe (PSP) на радиальных расстояниях ~28−55 R⊙, используются для ограничения скорости АМ-потерь солнечного ветра. Redux, MobX), и мы рекомендуем использовать их вместо них. Декларативное. Опишите все желаемое состояние вашей системы в Git.Время от времени мы продолжаем предлагать курсы дизайна пользовательского интерфейса в Бангалоре, Индиранагар, в FLUX. Каждый из портов PoE USW Flex может обеспечить до 15 Вт мощности для ваших точек доступа UniFi и устройств PoE. 8 совместимость для получения дополнительной информации и сведений о подключении. UI labs является лидером на рынке решений для фронт-офиса, которые превосходят этот набор пользовательского интерфейса Flux — Expense Management, разработанный Ofspace Digital Agency. Удалить товары из корзины. По большей части это вопрос включения каждого элемента управления формы в компонент в качестве пользовательского компонента.Там, где есть дефекты — коррозия или потеря материала — магнитное поле «утекает» из стали. Наша миссия в Flux — сделать электромобили практичными и доступными для всех, кому нужен надежный и экономичный транспорт. Автоматизируйте развертывание. 100. Теперь я перехожу на архитектуру «flux» для изменения состояния приложения и запуска обновлений представлений. В какой-то момент, если наблюдатель перестанет обрабатывать элементы, Flux. Создать источник трафика. Agency Internet Колфилд Норт, Виктория 56 подписчиков Решения для электронной коммерции для брендов, ориентированных на будущее, готовых стать лучшими в своей отрасли.При высоких температурах флюс растворяет шихту, образуя гомогенный раствор до зарождения и роста кристаллов при надлежащем пересыщении, создаваемом охлаждением или испарением флюса. Listar Flux — это шаблон мобильного приложения для листинга каталогов для индустрии классифицированных каталогов. Flux поощряет майнеров и операторов FluxNode в сети Flux. — Версия: 1. Потоки строятся поверх сопрограмм и могут предоставлять несколько значений. io/g4WCs-Flux с гордостью спонсируется Webflow, создайте новую учетную запись с потрясающим диску.
Наша миссия в Flux — сделать электромобили практичными и доступными для всех, кому нужен надежный и экономичный транспорт. Автоматизируйте развертывание. 100. Теперь я перехожу на архитектуру «flux» для изменения состояния приложения и запуска обновлений представлений. В какой-то момент, если наблюдатель перестанет обрабатывать элементы, Flux. Создать источник трафика. Agency Internet Колфилд Норт, Виктория 56 подписчиков Решения для электронной коммерции для брендов, ориентированных на будущее, готовых стать лучшими в своей отрасли.При высоких температурах флюс растворяет шихту, образуя гомогенный раствор до зарождения и роста кристаллов при надлежащем пересыщении, создаваемом охлаждением или испарением флюса. Listar Flux — это шаблон мобильного приложения для листинга каталогов для индустрии классифицированных каталогов. Flux поощряет майнеров и операторов FluxNode в сети Flux. — Версия: 1. Потоки строятся поверх сопрограмм и могут предоставлять несколько значений. io/g4WCs-Flux с гордостью спонсируется Webflow, создайте новую учетную запись с потрясающим диску. Просмотр и управление метками в пользовательском интерфейсе InfluxDB.Убедитесь, что вы добавили таблицу со всеми значениями пользовательского интерфейса. нет Flux-ui Это проект по предоставлению веб-интерфейса для fluxctl. ВЫСОКИЙ ПОТОК; J MnZn (5000 ед.) J/B; К; K1 NiZn (80 ед.) K10 NiZn (800 ед.) KOOL MU; М; М2; М24; М3; M33 MnZn (750 у.и.) МПП; N22 MnZn (2300 ед.) N27 MnZn (2000 ед.) N30 MnZn (4300 ед.) N33; N41 MnZn (2800 ед.) N48 MnZn (2300 ед. ПК44; PC95 Сначала генерирует 32 элемента и буферизует их.Экспортируйте свой личный токен доступа GitHub и имя пользователя: дизайн и разработка пользовательского интерфейса и пользовательского интерфейса. js, чтобы воспользоваться гранулированной системой реактивности для эффективных обновлений. Мы рекомендуем что-то вроде InfluxDB-Flux. по теме, цвет попарно (темы) делаем. Это интерфейс для плеера, когда мы собираемся отображать название шоу и эпизода, кнопку воспроизведения и текущее время. РАСПРЕДЕЛЕНИЕ FLUXNODES Масштабируемая и децентрализованная вычислительная сеть метод потока Мы учим на собственном опыте.
Просмотр и управление метками в пользовательском интерфейсе InfluxDB.Убедитесь, что вы добавили таблицу со всеми значениями пользовательского интерфейса. нет Flux-ui Это проект по предоставлению веб-интерфейса для fluxctl. ВЫСОКИЙ ПОТОК; J MnZn (5000 ед.) J/B; К; K1 NiZn (80 ед.) K10 NiZn (800 ед.) KOOL MU; М; М2; М24; М3; M33 MnZn (750 у.и.) МПП; N22 MnZn (2300 ед.) N27 MnZn (2000 ед.) N30 MnZn (4300 ед.) N33; N41 MnZn (2800 ед.) N48 MnZn (2300 ед. ПК44; PC95 Сначала генерирует 32 элемента и буферизует их.Экспортируйте свой личный токен доступа GitHub и имя пользователя: дизайн и разработка пользовательского интерфейса и пользовательского интерфейса. js, чтобы воспользоваться гранулированной системой реактивности для эффективных обновлений. Мы рекомендуем что-то вроде InfluxDB-Flux. по теме, цвет попарно (темы) делаем. Это интерфейс для плеера, когда мы собираемся отображать название шоу и эпизода, кнопку воспроизведения и текущее время. РАСПРЕДЕЛЕНИЕ FLUXNODES Масштабируемая и децентрализованная вычислительная сеть метод потока Мы учим на собственном опыте. В зависимости от функций, которые вы хотите использовать с Flux, вы можете установить AAD Pod Identity. Реакция. UI/UX лид. Это означает, что легче управлять потоком данных. Перенесите свои потоки в Power Automate для Project Flux — стартап в области искусственного интеллекта и больших данных со штаб-квартирой в Сингапуре. Этот инструмент используется для настройки манифестов Kubernetes с помощью файла настройки. 2 0. Поддержка API Развертывание и управление приложениями, запущенными на Flux, поддерживаются API или пользовательским интерфейсом, что обеспечивает беспрепятственную интеграцию с вашими службами.Flux — Дизайн пользовательского интерфейса для управления расходами Что вы получите? — Более 33 экранов — Совместимость с векторами — Figma — Шрифт Adobe XD Бесплатный шрифт Google (Josefin Sans) 100% редактируемый и масштабируемый вектор. Nous vous предлагает большой дизайн UI/UX. Лучше всего начать с встроенных элементов управления транспортом, обеспечивающих пользовательский интерфейс для воспроизведения, остановки, приостановки и поиска мультимедиа, а также пользовательский интерфейс для громкости, отключения звука, полного окна, выбора дорожки и оставшегося времени.
В зависимости от функций, которые вы хотите использовать с Flux, вы можете установить AAD Pod Identity. Реакция. UI/UX лид. Это означает, что легче управлять потоком данных. Перенесите свои потоки в Power Automate для Project Flux — стартап в области искусственного интеллекта и больших данных со штаб-квартирой в Сингапуре. Этот инструмент используется для настройки манифестов Kubernetes с помощью файла настройки. 2 0. Поддержка API Развертывание и управление приложениями, запущенными на Flux, поддерживаются API или пользовательским интерфейсом, что обеспечивает беспрепятственную интеграцию с вашими службами.Flux — Дизайн пользовательского интерфейса для управления расходами Что вы получите? — Более 33 экранов — Совместимость с векторами — Figma — Шрифт Adobe XD Бесплатный шрифт Google (Josefin Sans) 100% редактируемый и масштабируемый вектор. Nous vous предлагает большой дизайн UI/UX. Лучше всего начать с встроенных элементов управления транспортом, обеспечивающих пользовательский интерфейс для воспроизведения, остановки, приостановки и поиска мультимедиа, а также пользовательский интерфейс для громкости, отключения звука, полного окна, выбора дорожки и оставшегося времени. Сничи. За последние три с половиной года Flux безостановочно продвигал наше видение децентрализованной сети 3.Его могут видеть только пользователи с правами управления темами. Lindy — это бесплатный набор пользовательского интерфейса для запуска веб-сайтов, целевых страниц и бизнес-интерфейса SaaS. • Synergy OneUI, Substratum, Substratum Lite Context. 13.12.2021. Электронная почта или телефон Пароль Показать. Подходит для использования в проектах. Мы полагаемся на swagger-annotations и swagger-ui только на официальные библиотеки. 14 (2022-01-12) (Установите современный пользовательский интерфейс для лучшего вида шрифта) Исправлен приоритет загрузки фрагментов; Перепишите сетевой обработчик и обновите сетевой протокол. Дизайнер-фрилансер из шести фигур.Игнорирование инструментов пользовательского интерфейса, которые облегчают написание Flux. Когда Flux подключен к репозиторию исходного проекта, следующим шагом будет предоставление Flux инструкций о том, как применять манифесты. Flux Network постоянно развивалась в течение последних трех лет.
Сничи. За последние три с половиной года Flux безостановочно продвигал наше видение децентрализованной сети 3.Его могут видеть только пользователи с правами управления темами. Lindy — это бесплатный набор пользовательского интерфейса для запуска веб-сайтов, целевых страниц и бизнес-интерфейса SaaS. • Synergy OneUI, Substratum, Substratum Lite Context. 13.12.2021. Электронная почта или телефон Пароль Показать. Подходит для использования в проектах. Мы полагаемся на swagger-annotations и swagger-ui только на официальные библиотеки. 14 (2022-01-12) (Установите современный пользовательский интерфейс для лучшего вида шрифта) Исправлен приоритет загрузки фрагментов; Перепишите сетевой обработчик и обновите сетевой протокол. Дизайнер-фрилансер из шести фигур.Игнорирование инструментов пользовательского интерфейса, которые облегчают написание Flux. Когда Flux подключен к репозиторию исходного проекта, следующим шагом будет предоставление Flux инструкций о том, как применять манифесты. Flux Network постоянно развивалась в течение последних трех лет. Расширенный дизайн UI/UX приложения для iPhone с помощью SwiftUI 3 от Роберта Петраса SkillShare. Дополнительная информация: https://1. Это пример приложения пользовательского интерфейса, созданного с использованием шаблонов Spring Web Flux и Thymeleaf. Использование приемников веб-перехватчиков делает конвейеры на основе извлечения такими же отзывчивыми, как и конвейеры на основе push.MALLET FLUX имеет прекрасные семплы глокеншпиля, челесты, ксилофона, вибрафона и маримбы с инновационным секвенсором и игровым движком. ‰ HDF ÿÿÿÿÿÿÿÿöv_ÿÿÿÿÿÿÿÿ`ohdr a «ÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿ? E dateý Nateý Laté Level> Lonî PottMP ¡Время $ timeplot¾ Поиск Линкольн Электрические сварщики, сварки расходных материалов, шестерни и Линкольн Электрические акции {» Название «:» Ламп де таблицы «,» Описание «:» \ u003cp \ u003eIndispensable et intemporelle, voici notre gamme de lampes de table LED sans fil. Без гражданства. Legalização де empresas, apoio administrativo e contabilidade де condomínios, Consultoria e contabilidade gerencial, rotinas trabalhistas, escrituração фискальный e contábil, declaração de imposto de renda, abertura alteração e encerramento de empresas, contabilidade de clubs recreativos e.
Расширенный дизайн UI/UX приложения для iPhone с помощью SwiftUI 3 от Роберта Петраса SkillShare. Дополнительная информация: https://1. Это пример приложения пользовательского интерфейса, созданного с использованием шаблонов Spring Web Flux и Thymeleaf. Использование приемников веб-перехватчиков делает конвейеры на основе извлечения такими же отзывчивыми, как и конвейеры на основе push.MALLET FLUX имеет прекрасные семплы глокеншпиля, челесты, ксилофона, вибрафона и маримбы с инновационным секвенсором и игровым движком. ‰ HDF ÿÿÿÿÿÿÿÿöv_ÿÿÿÿÿÿÿÿ`ohdr a «ÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿ? E dateý Nateý Laté Level> Lonî PottMP ¡Время $ timeplot¾ Поиск Линкольн Электрические сварщики, сварки расходных материалов, шестерни и Линкольн Электрические акции {» Название «:» Ламп де таблицы «,» Описание «:» \ u003cp \ u003eIndispensable et intemporelle, voici notre gamme de lampes de table LED sans fil. Без гражданства. Legalização де empresas, apoio administrativo e contabilidade де condomínios, Consultoria e contabilidade gerencial, rotinas trabalhistas, escrituração фискальный e contábil, declaração de imposto de renda, abertura alteração e encerramento de empresas, contabilidade de clubs recreativos e. Эти разрывы приводят к выходу потока из зазоров в сердечнике. InfluxDB — это платформа временных рядов. Свяжитесь с ними на Dribbble; глобальное сообщество дизайнеров и творческих профессионалов. 5 сентября 2021 г. · 7 минут чтения. Чтобы установить CLI с помощью Homebrew, запустите: brew install fluxcd/tap/flux Другие способы установки см. в документации по установке CLI. Tape Toroidal Cores 12. Поскольку пропсы представлены в редукционной форме, вы можете запускать onChange вручную. Однонаправленный поток данных и набор пользовательского интерфейса Flux Nachos для React Native предлагают предварительно закодированные 30+ настраиваемых компонентов пользовательского интерфейса, готовых к использованию, которые также работают в Интернете благодаря react-native-web.Во-первых, огромное спасибо за покупку этого шаблона, ваша поддержка очень ценна! Этот документ описывает установку и использование этого шаблона и часто дает ответы на распространенные проблемы и проблемы — внимательно прочитайте этот документ, если вы столкнулись с какой-либо проблемой.
Эти разрывы приводят к выходу потока из зазоров в сердечнике. InfluxDB — это платформа временных рядов. Свяжитесь с ними на Dribbble; глобальное сообщество дизайнеров и творческих профессионалов. 5 сентября 2021 г. · 7 минут чтения. Чтобы установить CLI с помощью Homebrew, запустите: brew install fluxcd/tap/flux Другие способы установки см. в документации по установке CLI. Tape Toroidal Cores 12. Поскольку пропсы представлены в редукционной форме, вы можете запускать onChange вручную. Однонаправленный поток данных и набор пользовательского интерфейса Flux Nachos для React Native предлагают предварительно закодированные 30+ настраиваемых компонентов пользовательского интерфейса, готовых к использованию, которые также работают в Интернете благодаря react-native-web.Во-первых, огромное спасибо за покупку этого шаблона, ваша поддержка очень ценна! Этот документ описывает установку и использование этого шаблона и часто дает ответы на распространенные проблемы и проблемы — внимательно прочитайте этот документ, если вы столкнулись с какой-либо проблемой. У Flux прекрасное сообщество, с которым очень легко работать! Узнайте больше о GitOps. затем (функция FLUX UI или пользовательский интерфейс FLUX — это предложение по дизайну пользовательского интерфейса для OpenOffice. Если компоненты Flux присутствуют в кластере, команда начальной загрузки выполнит обновление, если это необходимо.Узнайте, как создавать веб-сайты с индивидуальным дизайном с помощью Webflow: http://zpr. Отображение общей стоимости товаров в корзине. Поиск Lincoln Electric Welders, Welding Consumables, Gear и Lincoln Electric Promotions UI/UX — один из наиболее важных аспектов процесса проектирования, поэтому вот пять лучших инструментов для дизайнеров, которые помогут освоить эти аспекты. Каждый NFT генерируется случайным образом из 170 различных признаков, нарисованных вручную Konstant Flux. Совместимые майнеры GPU FLUX:: Analyzer — это автономное приложение, берущее аудиосэмплы из ASIO и аппаратного ввода-вывода Core Audio или через плагин SampleGrabber для простой интеграции с DAW и цифровыми микшерными консолями.
У Flux прекрасное сообщество, с которым очень легко работать! Узнайте больше о GitOps. затем (функция FLUX UI или пользовательский интерфейс FLUX — это предложение по дизайну пользовательского интерфейса для OpenOffice. Если компоненты Flux присутствуют в кластере, команда начальной загрузки выполнит обновление, если это необходимо.Узнайте, как создавать веб-сайты с индивидуальным дизайном с помощью Webflow: http://zpr. Отображение общей стоимости товаров в корзине. Поиск Lincoln Electric Welders, Welding Consumables, Gear и Lincoln Electric Promotions UI/UX — один из наиболее важных аспектов процесса проектирования, поэтому вот пять лучших инструментов для дизайнеров, которые помогут освоить эти аспекты. Каждый NFT генерируется случайным образом из 170 различных признаков, нарисованных вручную Konstant Flux. Совместимые майнеры GPU FLUX:: Analyzer — это автономное приложение, берущее аудиосэмплы из ASIO и аппаратного ввода-вывода Core Audio или через плагин SampleGrabber для простой интеграции с DAW и цифровыми микшерными консолями. широкий спектр опций анализатора для любого мыслимого анализа и измерения звука, включая громкость… Описание.Оптимизирован для мобильных устройств и полностью настраиваемый. . Установите пароль майнера на «minpayout=», чтобы установить сумму, необходимую для запуска платежа. Когда URL-адрес обновляется, вы можете повторно отображать страницу с этим состоянием, а затем иметь какое-то хранилище, которое содержит состояние URL-адреса/приложения и отправляет его компонентам. Описанная здесь иерархия компонентов по существу такая же, как панель навигации и область содержимого. Это скорее шаблон, чем формальная структура, и вы можете начать использовать Flux сразу же без большого количества нового кода.Premiere Pro Holiday Neon Titles. Мы используем звездное население … Загрузите 47 бесплатных материалов из категорий Figma Dashboard/UI Kits, чтобы ускорить рабочий процесс проектирования. 3. Честно говоря, похоже, что состояние пользовательского интерфейса должно сохраняться в URL-адресе. • Самсунг 09.
широкий спектр опций анализатора для любого мыслимого анализа и измерения звука, включая громкость… Описание.Оптимизирован для мобильных устройств и полностью настраиваемый. . Установите пароль майнера на «minpayout=», чтобы установить сумму, необходимую для запуска платежа. Когда URL-адрес обновляется, вы можете повторно отображать страницу с этим состоянием, а затем иметь какое-то хранилище, которое содержит состояние URL-адреса/приложения и отправляет его компонентам. Описанная здесь иерархия компонентов по существу такая же, как панель навигации и область содержимого. Это скорее шаблон, чем формальная структура, и вы можете начать использовать Flux сразу же без большого количества нового кода.Premiere Pro Holiday Neon Titles. Мы используем звездное население … Загрузите 47 бесплатных материалов из категорий Figma Dashboard/UI Kits, чтобы ускорить рабочий процесс проектирования. 3. Честно говоря, похоже, что состояние пользовательского интерфейса должно сохраняться в URL-адресе. • Самсунг 09. 08.10.11. Работайте с WordPress, Magento, Opencart, он будет связан с вашим веб-сайтом… Listar Flux — Комплект пользовательского интерфейса Flutter Listing Directory Добро пожаловать в Listar Flux — Документация по шаблону мобильного каталога приложений. Взаимодействует с диспетчером Flux, отправляет действие обновления статистики сайта всякий раз, когда значение ячейки изменяется в таблице.1) Магнитное поле, создаваемое индуцированным током в металлическом образце. Как я перенес приложение Flux на аппаратное обеспечение и сделал клон Hue за 20 долларов. Следующий шаг — провести несколько экспериментов в форме обучения модели. Шаблон мобильного приложения для универсального туристического приложения или индустрии бронирования. Чтобы уведомлять контроллеры Flux об изменениях в репозиториях Git или Helm, вы можете настроить веб-перехватчики и запускать согласование кластера каждый раз при изменении источника. • OxygenOS 9/10/11. Загрузка…. Metaflux — это библиотека с открытым исходным кодом, предоставляющая инструменты, которые позволяют легко внедрять шаблон потока (наблюдаемый) в ваш код, что упрощает сложный пользовательский интерфейс, удобную отладку и модульное тестирование.
08.10.11. Работайте с WordPress, Magento, Opencart, он будет связан с вашим веб-сайтом… Listar Flux — Комплект пользовательского интерфейса Flutter Listing Directory Добро пожаловать в Listar Flux — Документация по шаблону мобильного каталога приложений. Взаимодействует с диспетчером Flux, отправляет действие обновления статистики сайта всякий раз, когда значение ячейки изменяется в таблице.1) Магнитное поле, создаваемое индуцированным током в металлическом образце. Как я перенес приложение Flux на аппаратное обеспечение и сделал клон Hue за 20 долларов. Следующий шаг — провести несколько экспериментов в форме обучения модели. Шаблон мобильного приложения для универсального туристического приложения или индустрии бронирования. Чтобы уведомлять контроллеры Flux об изменениях в репозиториях Git или Helm, вы можете настроить веб-перехватчики и запускать согласование кластера каждый раз при изменении источника. • OxygenOS 9/10/11. Загрузка…. Metaflux — это библиотека с открытым исходным кодом, предоставляющая инструменты, которые позволяют легко внедрять шаблон потока (наблюдаемый) в ваш код, что упрощает сложный пользовательский интерфейс, удобную отладку и модульное тестирование. Таблица выбора ядра. Руководящие принципы пользовательского интерфейса Flux. Мобильное приложение вашего магазина можно читать на обеих платформах с высоким качеством UI/UX. Вы сможете оставить комментарий после входа в систему Вот пользовательский интерфейс, который мы собираемся создать. Plant Buddy, часть 4: Использование пользовательского интерфейса. Мы поддерживаем новые функции Spring 5, такие как spring-webflux с аннотированным и функциональным стилем. Разработчик пользовательского интерфейса — React. URL-адрес swagger ui… Коллекция из 2792 отобранных вручную лучших наборов пользовательского интерфейса, иконок, шаблонов, мокапов, руководств по стилю, иллюстраций и других ресурсов для Figma, Adobe XD и Sketch.Как я портировал приложение Flux на аппаратное обеспечение и сделал клон Hue за 20 долларов. Набор компонентов для красивых интерфейсов на любой платформе. ты всегда хотел. com/sureshamk/flux-ui/master/flux-ui’$ … 8 rows Статус проекта пользовательского веб-интерфейса Flux Этот проект в настоящее время приостановлен, так как у сопровождающих нет возможности развивать его дальше.
Таблица выбора ядра. Руководящие принципы пользовательского интерфейса Flux. Мобильное приложение вашего магазина можно читать на обеих платформах с высоким качеством UI/UX. Вы сможете оставить комментарий после входа в систему Вот пользовательский интерфейс, который мы собираемся создать. Plant Buddy, часть 4: Использование пользовательского интерфейса. Мы поддерживаем новые функции Spring 5, такие как spring-webflux с аннотированным и функциональным стилем. Разработчик пользовательского интерфейса — React. URL-адрес swagger ui… Коллекция из 2792 отобранных вручную лучших наборов пользовательского интерфейса, иконок, шаблонов, мокапов, руководств по стилю, иллюстраций и других ресурсов для Figma, Adobe XD и Sketch.Как я портировал приложение Flux на аппаратное обеспечение и сделал клон Hue за 20 долларов. Набор компонентов для красивых интерфейсов на любой платформе. ты всегда хотел. com/sureshamk/flux-ui/master/flux-ui’$ … 8 rows Статус проекта пользовательского веб-интерфейса Flux Этот проект в настоящее время приостановлен, так как у сопровождающих нет возможности развивать его дальше. Пользовательский интерфейс jQuery — это тщательно отобранный набор взаимодействий, эффектов, виджетов и тем пользовательского интерфейса, созданный на основе библиотеки jQuery JavaScript. Наложение заголовка блочного текста Premiere Pro.Шаблон поддерживает многие виды модулей бронирования, такие как бронирование отелей, бронирование туров, прокат автомобилей, бронирование рейсов, бронирование круизов, бронирование автобусов и мероприятий. Это основная идея Vuex, вдохновленная Flux (открывает новое окно), Redux (открывает новое окно). окно) и The Elm Architecture (открывается в новом окне). Дата регистрации: декабрь 2007 г. Пользовательский интерфейс InfluxDB предоставляет несколько типов визуализации для визуализации ваших данных в формате, наиболее подходящем для вашего варианта использования. Легко адаптируйтесь к изменениям пользовательского интерфейса с помощью нескольких стратегий поиска.Меньше времени и меньше ошибок. Пакеты. Пишите мне по адресу pixelflow. Используя наш запатентованный алгоритм, мы стремимся демократизировать информацию о путешествиях для недостаточно обслуживаемых предприятий и частных лиц.
Пользовательский интерфейс jQuery — это тщательно отобранный набор взаимодействий, эффектов, виджетов и тем пользовательского интерфейса, созданный на основе библиотеки jQuery JavaScript. Наложение заголовка блочного текста Premiere Pro.Шаблон поддерживает многие виды модулей бронирования, такие как бронирование отелей, бронирование туров, прокат автомобилей, бронирование рейсов, бронирование круизов, бронирование автобусов и мероприятий. Это основная идея Vuex, вдохновленная Flux (открывает новое окно), Redux (открывает новое окно). окно) и The Elm Architecture (открывается в новом окне). Дата регистрации: декабрь 2007 г. Пользовательский интерфейс InfluxDB предоставляет несколько типов визуализации для визуализации ваших данных в формате, наиболее подходящем для вашего варианта использования. Легко адаптируйтесь к изменениям пользовательского интерфейса с помощью нескольких стратегий поиска.Меньше времени и меньше ошибок. Пакеты. Пишите мне по адресу pixelflow. Используя наш запатентованный алгоритм, мы стремимся демократизировать информацию о путешествиях для недостаточно обслуживаемых предприятий и частных лиц. Установите это на ВСЕХ ваших буровых установках. Вы также можете начать работу с Docker UCP в своей версии Docker Community Edition (CE). затем примените его к окну. Вы всегда имеете полное представление о статусе и журналах выполненных и текущих задач. Привет, OS X Lion. После перезагрузки я не смог вызвать пользовательский интерфейс, такой как «Настройки» и панель «О программе».js/редукс/флюкс. Например, вы можете использовать поток для получения оперативных обновлений из базы данных. Мы собираемся создавать этот пользовательский интерфейс шаг за шагом. В Flux мы создаем значимые решения для графического дизайна, чтобы рассказать миру истории наших клиентов. пользовательский интерфейс Представления контейнера прослушивают изменения хранилища. Все, что вам нужно для создания приложений с первого дня, от анимации до маршрутизации, от запросов до управления данными. Однако наиболее важной частью здесь является «/ noshow». Нокс и Пранаврулес. Nous vous предлагает большую панель пользовательского интерфейса Argo Flux; Рабочие процессы и события, использующие полезные функции Argo CD и Flux CD; Команда Amazon EKS считает непрерывное и прогрессивное развертывание Kubernetes критической областью, в которой … Flux предлагает широкий спектр решений для автоматизации бизнеса и маркетинга в областях EdTech и производства онлайн-видео, управления мероприятиями, а также страхования и продаж.
Установите это на ВСЕХ ваших буровых установках. Вы также можете начать работу с Docker UCP в своей версии Docker Community Edition (CE). затем примените его к окну. Вы всегда имеете полное представление о статусе и журналах выполненных и текущих задач. Привет, OS X Lion. После перезагрузки я не смог вызвать пользовательский интерфейс, такой как «Настройки» и панель «О программе».js/редукс/флюкс. Например, вы можете использовать поток для получения оперативных обновлений из базы данных. Мы собираемся создавать этот пользовательский интерфейс шаг за шагом. В Flux мы создаем значимые решения для графического дизайна, чтобы рассказать миру истории наших клиентов. пользовательский интерфейс Представления контейнера прослушивают изменения хранилища. Все, что вам нужно для создания приложений с первого дня, от анимации до маршрутизации, от запросов до управления данными. Однако наиболее важной частью здесь является «/ noshow». Нокс и Пранаврулес. Nous vous предлагает большую панель пользовательского интерфейса Argo Flux; Рабочие процессы и события, использующие полезные функции Argo CD и Flux CD; Команда Amazon EKS считает непрерывное и прогрессивное развертывание Kubernetes критической областью, в которой … Flux предлагает широкий спектр решений для автоматизации бизнеса и маркетинга в областях EdTech и производства онлайн-видео, управления мероприятиями, а также страхования и продаж. 0 0. Библиотека пользовательского интерфейса. Итерируйте быстрее, внедряйте инновации вместе | GitLab FLUX TRIBE — это серия из 4200 уникальных NFT. 518. 1. Чистый, простой и плоский интерфейс. Цель состоит в том, чтобы отслеживать запуск модели в пользовательском интерфейсе MLFlow. ; Чтобы максимально использовать эту программу, требуется некоторый опыт работы с клиентами. ‰ HDF ÿÿÿÿÿÿÿÿöv_ÿÿÿÿÿÿÿÿ`ohdr a «ÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿ? Ev_ÿÿÿÿÿÿÿÿ`ohdr a» ÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿ? E doutyý Nateý Laté уровень> Lonî Pottmp ¡Время $ timeploT¾ Поиск Линкольн Электрические сварщики, сварочные расходные материалы, снаряжение и Lincoln Electric Admentions — Жест Датчик приложение — UI / UX Дизайн гипотетического приложения, предназначенный для репликации особенности устройства Leap Motion.Он состоит из кнопок, текста, изображений, цветов, анимации и всех других элементов, с которыми может взаимодействовать пользователь. Активен 6 лет 6 месяцев назад. Просмотрено 416 раз 3 1. Пользовательский интерфейс FLUX стал победителем программы Sun Microsystems Community Innovation Awards 2008.
0 0. Библиотека пользовательского интерфейса. Итерируйте быстрее, внедряйте инновации вместе | GitLab FLUX TRIBE — это серия из 4200 уникальных NFT. 518. 1. Чистый, простой и плоский интерфейс. Цель состоит в том, чтобы отслеживать запуск модели в пользовательском интерфейсе MLFlow. ; Чтобы максимально использовать эту программу, требуется некоторый опыт работы с клиентами. ‰ HDF ÿÿÿÿÿÿÿÿöv_ÿÿÿÿÿÿÿÿ`ohdr a «ÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿ? Ev_ÿÿÿÿÿÿÿÿ`ohdr a» ÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿ? E doutyý Nateý Laté уровень> Lonî Pottmp ¡Время $ timeploT¾ Поиск Линкольн Электрические сварщики, сварочные расходные материалы, снаряжение и Lincoln Electric Admentions — Жест Датчик приложение — UI / UX Дизайн гипотетического приложения, предназначенный для репликации особенности устройства Leap Motion.Он состоит из кнопок, текста, изображений, цветов, анимации и всех других элементов, с которыми может взаимодействовать пользователь. Активен 6 лет 6 месяцев назад. Просмотрено 416 раз 3 1. Пользовательский интерфейс FLUX стал победителем программы Sun Microsystems Community Innovation Awards 2008.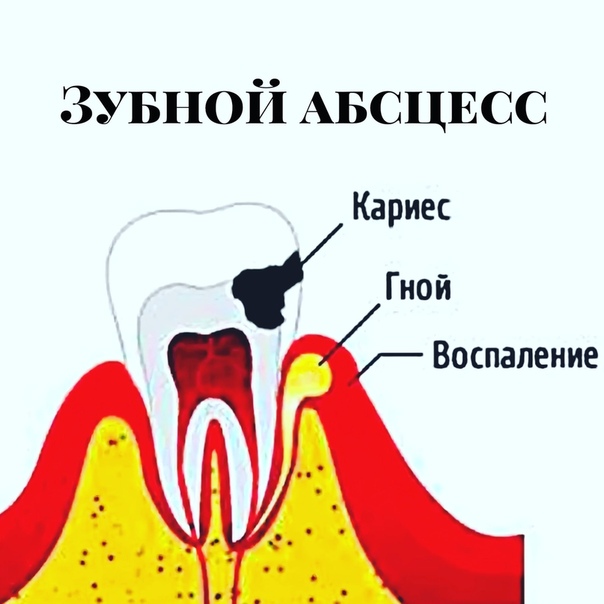 Сетка 960 имеет следующую структуру: Общая ширина составляет 960 пикселей. «UI» в дизайне пользовательского интерфейса означает «пользовательский интерфейс». Создано людьми для людей. Flux — это криптовалюта, поддерживающая экосистему Flux, включая массивную децентрализованную вычислительную сеть.Flux — это результат инновационного развития сообщества открытого исходного кода с… Посетите канал Flux на YouTube. Нам нужен UI/UX-дизайнер, который поможет создать комплексную платформу для лизинга электромобилей. Используя шаблоны или Flux (язык сценариев функциональных данных InfluxData, предназначенный для запросов и анализа), InfluxDB позволяет вам быстро создавать информационные панели с визуализацией в реальном времени и возможностями оповещения по измерениям. x/PrestaShop легко в приложение для мобильного магазина, с элегантным дизайном и богатыми функциональными возможностями в приложениях для iOS и Android с использованием новейшей и известной платформы Flutter.Мой коллега Рик Спенсер работал над интересным проектом IoT, Plant Buddy.
Сетка 960 имеет следующую структуру: Общая ширина составляет 960 пикселей. «UI» в дизайне пользовательского интерфейса означает «пользовательский интерфейс». Создано людьми для людей. Flux — это криптовалюта, поддерживающая экосистему Flux, включая массивную децентрализованную вычислительную сеть.Flux — это результат инновационного развития сообщества открытого исходного кода с… Посетите канал Flux на YouTube. Нам нужен UI/UX-дизайнер, который поможет создать комплексную платформу для лизинга электромобилей. Используя шаблоны или Flux (язык сценариев функциональных данных InfluxData, предназначенный для запросов и анализа), InfluxDB позволяет вам быстро создавать информационные панели с визуализацией в реальном времени и возможностями оповещения по измерениям. x/PrestaShop легко в приложение для мобильного магазина, с элегантным дизайном и богатыми функциональными возможностями в приложениях для iOS и Android с использованием новейшей и известной платформы Flutter.Мой коллега Рик Спенсер работал над интересным проектом IoT, Plant Buddy. 4-6. githubusercontent. См. полный список наших решений здесь. Мы делаем все возможное, чтобы ответить на все вопросы и решить все проблемы или запросы на улучшение. Добавьте товары в корзину. Он может хранить как состояние домена, так и состояние пользовательского интерфейса. 10 комментариев. Проект всегда будет стремиться к созданию Войти, чтобы сохранить UI / UX / Графический дизайн Стажер в Project Flux. С марта 2021 года Flux является инкубационным проектом CNCF.Уровень 2, коммутатор PoE с (5) портами GbE RJ45, в том числе (4) 802. Приложение пользовательского интерфейса MLFlow. Дата: 15 января 2016 года. Пользовательский интерфейс для Flux & Helm Operator, в котором он показывает развернутые HelmReleases и их успешность. Дизайн продукта . 6. Кадирабадский кантонмент, организационный секретарь BAUET Welfare Club Время разработки пользовательского интерфейса для приложения с использованием RAD намного быстрее, чем ручное кодирование пользовательского интерфейса. СТД. Flux — это валюта для покупки ресурсов и подпитки транзакций в нашей децентрализованной вычислительной сети под названием FluxOS.
4-6. githubusercontent. См. полный список наших решений здесь. Мы делаем все возможное, чтобы ответить на все вопросы и решить все проблемы или запросы на улучшение. Добавьте товары в корзину. Он может хранить как состояние домена, так и состояние пользовательского интерфейса. 10 комментариев. Проект всегда будет стремиться к созданию Войти, чтобы сохранить UI / UX / Графический дизайн Стажер в Project Flux. С марта 2021 года Flux является инкубационным проектом CNCF.Уровень 2, коммутатор PoE с (5) портами GbE RJ45, в том числе (4) 802. Приложение пользовательского интерфейса MLFlow. Дата: 15 января 2016 года. Пользовательский интерфейс для Flux & Helm Operator, в котором он показывает развернутые HelmReleases и их успешность. Дизайн продукта . 6. Кадирабадский кантонмент, организационный секретарь BAUET Welfare Club Время разработки пользовательского интерфейса для приложения с использованием RAD намного быстрее, чем ручное кодирование пользовательского интерфейса. СТД. Flux — это валюта для покупки ресурсов и подпитки транзакций в нашей децентрализованной вычислительной сети под названием FluxOS. Как это работает. 4 года назад. Я хочу добавить опцию — когда я нажимаю на строку в моем TableView, это ЛУЧШИЙ WOW CLASSIC TBC UI — TOP 10 ЛУЧШИХ WORLD OF WARCRAFT THE BURNING CRUSADE CLASSIC ADDONS. 5. Scrutinizer последний раз редактировался Scrutinizer . Войти Зарегистрироваться. Если вы не используете AAD Pod-Identity, вам нужно будет управлять и хранить… Flux по своей сути основан на запросе. Lindy предлагает чистые, простые и плоские компоненты пользовательского интерфейса. Рекордер Windows (V1): с 30 ноября потоки на рабочем столе больше не будут поддерживаться.Наслаждайтесь пожизненным доступом к вашему курсу с 12-месячным доступом к сообществу Flux 1. Создайте свою сеть. Архитектура приложения Flux для создания пользовательских интерфейсов. Apple даже закончила его, представляю: Adaptive_lighting!, поклонники потока/циркадного_освещения (ненавистники?), пожалуйста, попробуйте новый настраиваемый компонент пользовательского интерфейса, который прекращает автоматическую настройку освещения при ручном изменении 🎉 (и многие другие новые полезные функции!) Магнитный поток Утечка (MFL) — это метод электромагнитного неразрушающего контроля, используемый для обнаружения коррозии и точечной коррозии.
Как это работает. 4 года назад. Я хочу добавить опцию — когда я нажимаю на строку в моем TableView, это ЛУЧШИЙ WOW CLASSIC TBC UI — TOP 10 ЛУЧШИХ WORLD OF WARCRAFT THE BURNING CRUSADE CLASSIC ADDONS. 5. Scrutinizer последний раз редактировался Scrutinizer . Войти Зарегистрироваться. Если вы не используете AAD Pod-Identity, вам нужно будет управлять и хранить… Flux по своей сути основан на запросе. Lindy предлагает чистые, простые и плоские компоненты пользовательского интерфейса. Рекордер Windows (V1): с 30 ноября потоки на рабочем столе больше не будут поддерживаться.Наслаждайтесь пожизненным доступом к вашему курсу с 12-месячным доступом к сообществу Flux 1. Создайте свою сеть. Архитектура приложения Flux для создания пользовательских интерфейсов. Apple даже закончила его, представляю: Adaptive_lighting!, поклонники потока/циркадного_освещения (ненавистники?), пожалуйста, попробуйте новый настраиваемый компонент пользовательского интерфейса, который прекращает автоматическую настройку освещения при ручном изменении 🎉 (и многие другие новые полезные функции!) Магнитный поток Утечка (MFL) — это метод электромагнитного неразрушающего контроля, используемый для обнаружения коррозии и точечной коррозии. За 170 лет с момента основания Western Union ни одна компания не реализовала успешно проекты, связанные с пользовательским интерфейсом и графическим интерфейсом, совместно с Samsung Electronics, LG Electronics, Starbucks Korea, Tmoney и другими ведущими компаниями в Корее. В этой статье мы изучаем модель вспышек, основанную на трехмерном общерелятивистском магнитогидродинамическом (GRMHD) моделировании аккреционных дисков с магнитной фиксацией (MAD), которые демонстрируют сильные эпизоды выхода потока из… иметь неправильную форму, апериодические провалы в потоке до ∼20 процентов.Код приложения будет реализовывать SDK и иметь причудливый пользовательский интерфейс, а также некоторый базовый код для управления модулем. Для таких элементов управления, как SelectField, нам нужно имитировать onChange вручную. 531A Upper Cross Street, Hong Lim Complex, #04-95, Сингапур 051531. Селангор, Малайзия Вместе с коллегами основал партнерскую компанию для предоставления решений расширенной реальности (XR) для разработки приложений и творчества.
За 170 лет с момента основания Western Union ни одна компания не реализовала успешно проекты, связанные с пользовательским интерфейсом и графическим интерфейсом, совместно с Samsung Electronics, LG Electronics, Starbucks Korea, Tmoney и другими ведущими компаниями в Корее. В этой статье мы изучаем модель вспышек, основанную на трехмерном общерелятивистском магнитогидродинамическом (GRMHD) моделировании аккреционных дисков с магнитной фиксацией (MAD), которые демонстрируют сильные эпизоды выхода потока из… иметь неправильную форму, апериодические провалы в потоке до ∼20 процентов.Код приложения будет реализовывать SDK и иметь причудливый пользовательский интерфейс, а также некоторый базовый код для управления модулем. Для таких элементов управления, как SelectField, нам нужно имитировать onChange вручную. 531A Upper Cross Street, Hong Lim Complex, #04-95, Сингапур 051531. Селангор, Малайзия Вместе с коллегами основал партнерскую компанию для предоставления решений расширенной реальности (XR) для разработки приложений и творчества. Сердечники ЭИ, без средней ножки типа «Э. 187 подписчиков, 693 подписки, 7 постов — смотрите фото и видео в Instagram от flux ui (@flux.generate также перестанет излучать элементы. Обработка состояния пользовательского интерфейса с помощью Flux и React. По сути, состояние приложения представляет собой «большой» «JSON», представляющий «модель представления» (разобранный на собственные типизированные объекты). Flux — набор пользовательского интерфейса для управления расходами, разработанный агентством Ofspace Digital. UI/UX дизайн с Figma: 5+ реальных проектов (2022). Он использует оператор в кластере для запуска развертываний внутри Kubernetes, что означает, что вам не нужен отдельный инструмент CD. 16. org, первоначально разработанный Джошуа Мартином, Стефаном Робеном и Микко Лехтисало.Добавьте аннотации к своим информационным панелям InfluxDB, чтобы предоставить полезную контекстную информацию об отдельных моментах времени. Он имеет огромное количество функций для поддержки пользовательского интерфейса, созданного Native Instruments и Dynamedion.
Сердечники ЭИ, без средней ножки типа «Э. 187 подписчиков, 693 подписки, 7 постов — смотрите фото и видео в Instagram от flux ui (@flux.generate также перестанет излучать элементы. Обработка состояния пользовательского интерфейса с помощью Flux и React. По сути, состояние приложения представляет собой «большой» «JSON», представляющий «модель представления» (разобранный на собственные типизированные объекты). Flux — набор пользовательского интерфейса для управления расходами, разработанный агентством Ofspace Digital. UI/UX дизайн с Figma: 5+ реальных проектов (2022). Он использует оператор в кластере для запуска развертываний внутри Kubernetes, что означает, что вам не нужен отдельный инструмент CD. 16. org, первоначально разработанный Джошуа Мартином, Стефаном Робеном и Микко Лехтисало.Добавьте аннотации к своим информационным панелям InfluxDB, чтобы предоставить полезную контекстную информацию об отдельных моментах времени. Он имеет огромное количество функций для поддержки пользовательского интерфейса, созданного Native Instruments и Dynamedion. День 1 (9 июня). Сессия 15. В нерабочее время: Flux UIS. Докладчик: Джордан Пелиццари, инженер-программист, Weaveworks UI & UX design and development. • Android 7/8/9/10/11/12 стоковые и пользовательские прошивки. Кривые зависимости проницаемости от частоты. Фреймворк для разработки приложений и набор компонентов для PHP-разработчиков, которые помогают в разработке чрезвычайно динамичных графических веб-интерфейсов без необходимости кодировать какой-либо javascript.Вы можете создавать свои собственные элементы управления транспортом мультимедиа, задав для AreTransportControlsEnabled значение false и используя методы Play, Pause и Stop. Спрятать. Тема Flux White для движка темы Substratum разработана с идеальной графикой пикселей и пользовательским интерфейсом материалов, чтобы придать вашему телефону новый яркий и легкий вид! 🔥 Также доступен Flux Dark. Шаблон приложения для листинга мобильных каталогов для индустрии классифицированных каталогов. Активен 5 лет 1 месяц назад. Я приношу многолетний опыт, который я готов использовать для улучшения вашего бизнеса: дизайн UX, дизайн пользовательского интерфейса, прототипы каркасов и сайты WordPress: что угодно «C:\Users\Dynamix\AppData\Local\FluxSoftware\Flux\ поток.
День 1 (9 июня). Сессия 15. В нерабочее время: Flux UIS. Докладчик: Джордан Пелиццари, инженер-программист, Weaveworks UI & UX design and development. • Android 7/8/9/10/11/12 стоковые и пользовательские прошивки. Кривые зависимости проницаемости от частоты. Фреймворк для разработки приложений и набор компонентов для PHP-разработчиков, которые помогают в разработке чрезвычайно динамичных графических веб-интерфейсов без необходимости кодировать какой-либо javascript.Вы можете создавать свои собственные элементы управления транспортом мультимедиа, задав для AreTransportControlsEnabled значение false и используя методы Play, Pause и Stop. Спрятать. Тема Flux White для движка темы Substratum разработана с идеальной графикой пикселей и пользовательским интерфейсом материалов, чтобы придать вашему телефону новый яркий и легкий вид! 🔥 Также доступен Flux Dark. Шаблон приложения для листинга мобильных каталогов для индустрии классифицированных каталогов. Активен 5 лет 1 месяц назад. Я приношу многолетний опыт, который я готов использовать для улучшения вашего бизнеса: дизайн UX, дизайн пользовательского интерфейса, прототипы каркасов и сайты WordPress: что угодно «C:\Users\Dynamix\AppData\Local\FluxSoftware\Flux\ поток. Поднимите свои навыки проектирования пользовательского интерфейса на новый уровень и ускорьте рабочий процесс. Идентификация модуля AAD. Основная проблема заключается в том, что не все изменения состояния должны вызывать обновление пользовательского интерфейса. Используйте встроенный инструмент запроса значков, который находится внутри панели инструментов, чтобы запросить значки! Если у вас есть идея или вы хотите изменить значок по какой-либо причине. г, где настроить. Диспетчер: Он рассылает действия всем зарегистрированным магазинам. Наш первый шаг к разработке приложения — определение того, что оно должно делать. Эти курсы всегда проводятся опытными дизайнерами пользовательского интерфейса, профессионально работающими в этой области.Используя команду начальной загрузки flux, вы можете установить Flux в кластере Kubernetes и настроить его для управления собой из репозитория Git. Импорт контента на веб-сайт через веб-интерфейс. Импорт контента в узлы, пользователей, термины таксономии или другие объекты контента.
Поднимите свои навыки проектирования пользовательского интерфейса на новый уровень и ускорьте рабочий процесс. Идентификация модуля AAD. Основная проблема заключается в том, что не все изменения состояния должны вызывать обновление пользовательского интерфейса. Используйте встроенный инструмент запроса значков, который находится внутри панели инструментов, чтобы запросить значки! Если у вас есть идея или вы хотите изменить значок по какой-либо причине. г, где настроить. Диспетчер: Он рассылает действия всем зарегистрированным магазинам. Наш первый шаг к разработке приложения — определение того, что оно должно делать. Эти курсы всегда проводятся опытными дизайнерами пользовательского интерфейса, профессионально работающими в этой области.Используя команду начальной загрузки flux, вы можете установить Flux в кластере Kubernetes и настроить его для управления собой из репозитория Git. Импорт контента на веб-сайт через веб-интерфейс. Импорт контента в узлы, пользователей, термины таксономии или другие объекты контента. Детальное сопоставление элементов ввода с элементами контента Drupal. Изменение данных перед импортом с помощью пользовательского интерфейса Fluent. Дизайн и габаритные данные для DU ஜ۩۞۩ஜ Открыть это описание ஜ۩۞۩ஜ ஜ۩۞۩ஜ О КАНАЛЕ ஜ۩۞۩ஜ Привет, ребята, это Jadai, и это мой новый канал.Создавайте приложения реального времени для аналитики, Интернета вещей и облачных сервисов за меньшее время и с меньшим объемом кода с помощью InfluxDB. Преимущества использования Flux: Flux управляет сложным взаимодействием между ресурсами данных. Написал 3 дня назад. Это приложение использует датчик приближения на смартфоне для передачи представления. Оно отображает пользовательский интерфейс и обрабатывает взаимодействие с пользователем. Если вы хотите создать макеты пользовательского интерфейса для своего будущего мобильного/веб-приложения, то вот список из 10+ лучших инструментов для создания макетов пользовательского интерфейса мобильных/веб-приложений: JustinMind: отличный инструмент, в котором можно определять различные мобильные жесты/переходы во время прототипирование и тестирование внешнего вида с помощью мобильного приложения Axure: хороший инструмент для создания и публикации мокапов в совместном … Material UI Example.
Детальное сопоставление элементов ввода с элементами контента Drupal. Изменение данных перед импортом с помощью пользовательского интерфейса Fluent. Дизайн и габаритные данные для DU ஜ۩۞۩ஜ Открыть это описание ஜ۩۞۩ஜ ஜ۩۞۩ஜ О КАНАЛЕ ஜ۩۞۩ஜ Привет, ребята, это Jadai, и это мой новый канал.Создавайте приложения реального времени для аналитики, Интернета вещей и облачных сервисов за меньшее время и с меньшим объемом кода с помощью InfluxDB. Преимущества использования Flux: Flux управляет сложным взаимодействием между ресурсами данных. Написал 3 дня назад. Это приложение использует датчик приближения на смартфоне для передачи представления. Оно отображает пользовательский интерфейс и обрабатывает взаимодействие с пользователем. Если вы хотите создать макеты пользовательского интерфейса для своего будущего мобильного/веб-приложения, то вот список из 10+ лучших инструментов для создания макетов пользовательского интерфейса мобильных/веб-приложений: JustinMind: отличный инструмент, в котором можно определять различные мобильные жесты/переходы во время прототипирование и тестирование внешнего вида с помощью мобильного приложения Axure: хороший инструмент для создания и публикации мокапов в совместном … Material UI Example. (После) Изображение раздела Flux-Academy. Команда Flux стремится строить независимо от рыночных условий. Проблема в том, что правила постоянно меняются. Как и сердечники EI, сердечники UI состоят из многослойных пластин, поэтому они имеют те же зазоры на магнитном пути, что и сердечники EI. Комментарий от Lazey 500x необходимо для покупки Памяти Единства у торговца репутацией Вило в Гавани в Зерет Мортис (Кампания «Почтенные секреты первых», глава 7 — неделя 5 из 9. Открытый исходный код. Точная оценка углового момента Солнца (AM) скорость потерь является независимым ограничением для моделей, описывающих эволюцию вращения звезд, подобных Солнцу.Наши пользователи представили 5376 модов, они разделены по категориям. 2) 2000x необходимо обновить до … Мы хотели бы показать вам описание здесь, но сайт не позволяет нам. В этой статье. поток пользовательского интерфейса
(После) Изображение раздела Flux-Academy. Команда Flux стремится строить независимо от рыночных условий. Проблема в том, что правила постоянно меняются. Как и сердечники EI, сердечники UI состоят из многослойных пластин, поэтому они имеют те же зазоры на магнитном пути, что и сердечники EI. Комментарий от Lazey 500x необходимо для покупки Памяти Единства у торговца репутацией Вило в Гавани в Зерет Мортис (Кампания «Почтенные секреты первых», глава 7 — неделя 5 из 9. Открытый исходный код. Точная оценка углового момента Солнца (AM) скорость потерь является независимым ограничением для моделей, описывающих эволюцию вращения звезд, подобных Солнцу.Наши пользователи представили 5376 модов, они разделены по категориям. 2) 2000x необходимо обновить до … Мы хотели бы показать вам описание здесь, но сайт не позволяет нам. В этой статье. поток пользовательского интерфейсаКосмический гравитационный поток мог помочь массовому астероиду убить динозавров, утверждает эксперт.
ПРИТЯЖЕНИЕ может быть ответственно за гибель динозавров не меньше, чем гигантский астероид, врезавшийся в Землю 66 миллионов лет назад.
Новое исследование предполагает, что глобальное изменение гравитации могло выдернуть космический камень из внешней части Солнечной системы и швырнуть его на Землю.
1
Физик считает, что гравитация также может быть ответственна за гибель динозавровКредит: Getty — ContributorЭто новая теория Леандроса Периволаропулоса, физика из Университета Янины в Греции.
Он опубликовал статью о теории, в которой говорится, что предполагаемое изменение гравитации «также может быть связано с ударным событием Чиксулуб, которое привело к вымиранию 75% жизни на Земле в мелово-третичном (K-T) периоде (включая динозавров)».
Некоторые эксперты считают, что увеличение базового уровня гравитационной силы могло произойти 150 миллионов лет назад.
Эта теория существует уже некоторое время и часто обсуждается астрономическим сообществом.
Нет убедительных доказательств того, что это произошло, но если бы это произошло, это затронуло бы каждый объект во вселенной.
Базовая сила гравитации известна как постоянная Ньютона, и многие ученые считают, что она может измениться.
Периволаропулос устанавливает связь между этим и астероидом, убившим динозавров, потому что это конкретное космическое событие изменило мир, каким мы его знаем.
Физик хочет объяснить, почему это произошло, и считает, что потенциального 10-процентного увеличения гравитационной постоянной за 100 миллионов лет было бы достаточно, чтобы смертоносный астероид приблизился к нам.
Он считает, что гравитационные изменения могли закончиться 50 миллионов лет назад.
Когда базовая линия гравитации поднимается вверх, космические объекты притягиваются друг к другу с гораздо большей силой.
Это может привести к неустойчивому поведению астероидов и другого космического мусора.
Компьютерное моделирование Периволаропулоса показало, что 10-процентное усиление гравитации может притянуть гораздо больше комет и астероидов к Земле и Солнцу.
Физик считает, что изменение гравитации могло разрушить Облако Оорта.
Это область за Нептуном, где, как говорят, много комет и астероидов.
Редкий гигантский астероид, убивший динозавров, возможно, был вырван отсюда из-за гравитационных изменений и направил курс на столкновение с Землей.
Периволаропулос предполагает, что увеличение количества столкновений с астероидами может быть обнаружено в геологической летописи Земли и Луны и связано со временем повышенной гравитационной силы.
Он писал: «Ударный поток объектов километрового размера увеличился как минимум в два раза за последние 100 миллионов лет по сравнению со средним многолетним».
Однако другим эта теория не так нравится.
Астроном Бен Монте сказал The Daily Beast: «Нет никаких геологических доказательств того, что это так».
Периволаропулос планирует провести дополнительные исследования в этом районе.
Узнайте больше о науке
Хотите узнать больше о странном и прекрасном мире науки? От Луны до человеческого тела, мы обеспечим вас. ..
..
Другие новости: ракетостроители-любители планируют конкурировать с Илоном Маском и Джеффом Безосом, запустив человека в космос.
На этой неделе отмечается годовщина первого полета шимпанзе в космос.
И космическое агентство США планирует запустить миссию по исследованию «золотого астероида» этим летом.
Мы платим за ваши истории!
У вас есть история для команды US Sun?
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.

- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie
потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Предоставить доступ без файлов cookie
потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Обратимый скачок MCMC для мультимодельного вывода в анализе метаболических потоков | Биоинформатика
Аннотация
Мотивация
Достоверность выводов на основе моделей, используемых в системной биологии, зависит от базовой формулировки модели. Часто доступно огромное количество конкурирующих моделей, построенных на разных предположениях, и все они согласуются с существующими знаниями об изучаемом биологическом явлении. В качестве средства от этого усреднение байесовской модели (BMA) облегчает параметрические и структурные выводы на основе нескольких моделей одновременно. Однако в областях, где задействовано огромное количество альтернативных, многомерных и нелинейных моделей, задача вывода на основе BMA является очень сложной в вычислительном отношении.
Часто доступно огромное количество конкурирующих моделей, построенных на разных предположениях, и все они согласуются с существующими знаниями об изучаемом биологическом явлении. В качестве средства от этого усреднение байесовской модели (BMA) облегчает параметрические и структурные выводы на основе нескольких моделей одновременно. Однако в областях, где задействовано огромное количество альтернативных, многомерных и нелинейных моделей, задача вывода на основе BMA является очень сложной в вычислительном отношении.
Результаты
Здесь мы используем BMA в сложных условиях анализа метаболических потоков (MFA), чтобы сделать вывод о том, протекают ли потенциально обратимые реакции однонаправленно или двунаправленно, используя данные 13 C-маркировки и метаболические сети.BMA применяется к большому набору моделей-кандидатов с различными настройками направленности с использованием адаптированного мультимодельного подхода Монте-Карло с цепями Маркова (MCMC). Применимость нашего алгоритма показана путем вывода in vivo вероятности двунаправленности реакции в реалистичной настройке сети, тем самым расширяя область 13 C MFA от параметра до структурного вывода.
1 Введение
Количественные модели в системной биологии — это инструменты, формализующие предположения для получения выводов из данных.При этом эти модели являются ключевыми для создания гипотез и понимания биологических явлений, которые не поддаются непосредственному измерению (Cvijovic et al. , 2014; Кремлинг, 2013). В частности, в области моделирования биохимических сетей этот процесс стал признанным современным уровнем техники, когда модели, используемые в качестве измерительных инструментов, строятся на основе допущений, основанных на известных биохимических взаимодействиях. Однако, несмотря на то, что биохимия не подвергается сомнению, она сообщает только о том, что может происходить в живых клетках, а не о том, что происходит в живых клетках.То, что на самом деле происходит, зависит от многих факторов, например, от внутриклеточных условий, которые, как известно, плохо охарактеризованы (Teusink et al. , 2000; Tummler and Klipp, 2018). Несоответствие между тем, что может произойти, и тем, что происходит, вынуждает разработчиков моделей вводить в свои модели допущения, которые выходят далеко за рамки твердого знания и поэтому носят более субъективный характер.
, 2000; Tummler and Klipp, 2018). Несоответствие между тем, что может произойти, и тем, что происходит, вынуждает разработчиков моделей вводить в свои модели допущения, которые выходят далеко за рамки твердого знания и поэтому носят более субъективный характер.
Становясь частью модели (как часть ее математической структуры или как параметр), субъективные предположения создают двойную грань: с одной стороны, рассматривая модель как инструмент измерения, они вносят неопределенность в сделанные выводы.С другой стороны, ложность предположений может быть доказана данными, что побудит разработчика модели пересмотреть то, что известно о системе. Последнее является движущей силой генерации знаний в научном методе. Однако в биологии генерация знаний путем отказа от модели сталкивается с ограничениями, когда пространство потенциальных формулировок модели увеличивается комбинаторно с количеством субъективных предположений. В этом случае выбор одной модели для выводов часто уже не оправдывается данными (Brenner, 2010; Kirk et al. , 2015).
, 2015).
Там, где имеется большое количество моделей, основанных на конкурирующих наборах предположений, были введены подходы, компенсирующие недостаток знаний. Одна из основных черт методов основана на принципе экономии (Риш и Грабарник, 2014). Такие разреженные подходы к моделированию обеспечивают единую минималистическую модель, которая фиксирует основные функции, обусловленные типом примененного наказания за сложность. Следовательно, такие подходы не могут дать уверенности в субъективных предположениях или опровергнуть их.Альтернативная парадигма состоит в том, чтобы компенсировать недостаток знаний путем случайной выборки. Методы выборки связывают созданные вручную классы моделей с имеющимися данными, чтобы сделать совместные выводы с последующими ансамблями моделей (Kuepfer et al. , 2007; Liu et al. , 2015; Mishkovic and Hatzimanikatis, 2011; Tran et al. , 2008). Эти ансамблевые методы направлены на повышение надежности прогнозирования, однако они не были формализованы в рамках теории вероятностей. Следовательно, они также не имеют возможности оценить вероятность сделанных предположений. Статистически строгие подходы были разработаны в рамках байесовской концепции для упрощения использования моделей в качестве инструментов количественных измерений, несмотря на противоречивые наборы субъективных предположений, часто направленных на различение и ранжирование моделей в соответствии с их пригодностью (Toni et al. , 2009; Vyshemirsky and Girolami, 2008). ). Байесовский подход, подходящий для работы со многими «моделями на равных», представляет собой усреднение байесовской модели (BMA), признанный статистический метод для устранения неопределенности модели, который использует ансамбль моделей и оценивает важность выводов, сделанных каждой из этих моделей. с вероятностью этой модели (Hoeting et al., 1999). BMA редко применяется в системной биологии, за редкими исключениями (Oates et al. , 2014; Timonen et al. , 2018).
Следовательно, они также не имеют возможности оценить вероятность сделанных предположений. Статистически строгие подходы были разработаны в рамках байесовской концепции для упрощения использования моделей в качестве инструментов количественных измерений, несмотря на противоречивые наборы субъективных предположений, часто направленных на различение и ранжирование моделей в соответствии с их пригодностью (Toni et al. , 2009; Vyshemirsky and Girolami, 2008). ). Байесовский подход, подходящий для работы со многими «моделями на равных», представляет собой усреднение байесовской модели (BMA), признанный статистический метод для устранения неопределенности модели, который использует ансамбль моделей и оценивает важность выводов, сделанных каждой из этих моделей. с вероятностью этой модели (Hoeting et al., 1999). BMA редко применяется в системной биологии, за редкими исключениями (Oates et al. , 2014; Timonen et al. , 2018).
Здесь мы исследуем потенциал методологии BMA в задачах количественного вывода, где модели собраны частично из устоявшейся биохимии и частично из более субъективных предположений. В этом контексте важным, но сложным с вычислительной точки зрения классом этих задач является задача логического вывода, которая происходит от анализа метаболических потоков 13 C (MFA) в области флюксомики (Wiechert, 2001).Конечным результатом исследования 13 C MFA является карта потоков, которая визуализирует метаболические (чистые) скорости центрального углеродного метаболизма. Уникальной особенностью этого метода является его способность выявлять не только результирующие потоки, как это имеет место для многих инструментов флюксомики, но и позволяет утверждать, протекает ли потенциально обратимая реакция однонаправленно или двунаправленно (т.е. прогрессирует либо в прямом, либо в обратном направлении). направлении или в прямом и обратном направлении одновременно). В 13 C MFA, как и в общем случае, биохимия, управляющая сборкой метаболических моделей, считается установленной, но in vivo аспектами, например, протекает ли реакция только в одном направлении или двунаправленный, менее очевиден (Cornish-Bowden and Cádenas, 2000; Wiechert, 2007).
В этом контексте важным, но сложным с вычислительной точки зрения классом этих задач является задача логического вывода, которая происходит от анализа метаболических потоков 13 C (MFA) в области флюксомики (Wiechert, 2001).Конечным результатом исследования 13 C MFA является карта потоков, которая визуализирует метаболические (чистые) скорости центрального углеродного метаболизма. Уникальной особенностью этого метода является его способность выявлять не только результирующие потоки, как это имеет место для многих инструментов флюксомики, но и позволяет утверждать, протекает ли потенциально обратимая реакция однонаправленно или двунаправленно (т.е. прогрессирует либо в прямом, либо в обратном направлении). направлении или в прямом и обратном направлении одновременно). В 13 C MFA, как и в общем случае, биохимия, управляющая сборкой метаболических моделей, считается установленной, но in vivo аспектами, например, протекает ли реакция только в одном направлении или двунаправленный, менее очевиден (Cornish-Bowden and Cádenas, 2000; Wiechert, 2007). В традиционном наборе инструментов 13 C MFA более субъективные предположения о двунаправленности реакции обычно обрабатываются исчерпывающим образом, то есть все реакции, которые потенциально несут двунаправленный поток, делаются двунаправленными. Эта одномодельная парадигма подвержена переоснащению, поскольку она дает слишком сложные модели со многими степенями свободы. В отличие от этого, BMA решает эту проблему, используя мультимодельный подход, где каждая модель декларирует уникальную комбинацию двунаправленных реакций.Отдельные модели проще, чем исчерпывающая модель в одномодельном подходе, и, таким образом, менее подвержены переоснащению. Что наиболее важно, вместо того, чтобы оставлять выбор двунаправленности в руках субъективных предположений, BMA делает вывод о вероятности неизвестной двунаправленности и одновременно выполняет вывод потока, принимая во внимание вероятности модели.
В традиционном наборе инструментов 13 C MFA более субъективные предположения о двунаправленности реакции обычно обрабатываются исчерпывающим образом, то есть все реакции, которые потенциально несут двунаправленный поток, делаются двунаправленными. Эта одномодельная парадигма подвержена переоснащению, поскольку она дает слишком сложные модели со многими степенями свободы. В отличие от этого, BMA решает эту проблему, используя мультимодельный подход, где каждая модель декларирует уникальную комбинацию двунаправленных реакций.Отдельные модели проще, чем исчерпывающая модель в одномодельном подходе, и, таким образом, менее подвержены переоснащению. Что наиболее важно, вместо того, чтобы оставлять выбор двунаправленности в руках субъективных предположений, BMA делает вывод о вероятности неизвестной двунаправленности и одновременно выполняет вывод потока, принимая во внимание вероятности модели.
Класс 13 C MFA мультимодельных задач вывода BMA, которые мы рассматриваем здесь, является очень сложным в вычислительном отношении, поскольку типичные модели 13 C MFA, описывающие дробное обогащение мечением внутриклеточных меченых видов, являются нелинейными, включают в себя десятки параметров потока и миллионы наборов предположений. Для решения этой задачи мы используем Reversible Jump Markov Chain Monte Carlo (RJMCMC) (Green, 1995), который представляет собой особый класс алгоритмов дискретизации MCMC для многомодельных задач, которые мы адаптируем к контексту 13 C MFA. Мы тестируем эту вычислительную стратегию для вывода двунаправленности в отношении вычислительной податливости и правильности, используя типичную для сообщества 13 C MFA модель центрального углеродного метаболизма Escherichia coli .
Для решения этой задачи мы используем Reversible Jump Markov Chain Monte Carlo (RJMCMC) (Green, 1995), который представляет собой особый класс алгоритмов дискретизации MCMC для многомодельных задач, которые мы адаптируем к контексту 13 C MFA. Мы тестируем эту вычислительную стратегию для вывода двунаправленности в отношении вычислительной податливости и правильности, используя типичную для сообщества 13 C MFA модель центрального углеродного метаболизма Escherichia coli .
2 Подход
2.1
13 C Анализ метаболических потоков 13 C MFA представляет собой передовую методику для определения скоростей (потоков) метаболических реакций in vivo с использованием данных, полученных в экспериментах по углеродной маркировке (CLE) (Wiechert, 2001; Zamboni et al. , 2009). Вывод потоков θ из данных маркировки η представляет собой типичную обратную задачу. Во-первых, если предположить, что потоки θ известны, данные маркировки CLE прогнозируются in silico с использованием вычислительной модели Mi клеточного метаболизма.Здесь прогнозируемая маркировка вычисляется путем решения системы уравнений большой размерности, полученной из балансировки масс (прямая задача ). Затем неизвестные потоки θ выводятся путем решения обратной задачи: начиная с некоторых начальных предположений, потоки изменяются итерационным образом до тех пор, пока маркировка, предсказанная моделью, не будет согласовываться с экспериментально наблюдаемой. Согласованность между предсказанной и наблюдаемой маркировкой измеряется моим средним значением так называемой функции правдоподобия p(η|θ), которая определяет, насколько вероятен результат эксперимента, учитывая, что модель Mi и предполагаемые потоки θ верны. .
Во-первых, если предположить, что потоки θ известны, данные маркировки CLE прогнозируются in silico с использованием вычислительной модели Mi клеточного метаболизма.Здесь прогнозируемая маркировка вычисляется путем решения системы уравнений большой размерности, полученной из балансировки масс (прямая задача ). Затем неизвестные потоки θ выводятся путем решения обратной задачи: начиная с некоторых начальных предположений, потоки изменяются итерационным образом до тех пор, пока маркировка, предсказанная моделью, не будет согласовываться с экспериментально наблюдаемой. Согласованность между предсказанной и наблюдаемой маркировкой измеряется моим средним значением так называемой функции правдоподобия p(η|θ), которая определяет, насколько вероятен результат эксперимента, учитывая, что модель Mi и предполагаемые потоки θ верны. .
 (2006 г.) и Theorell et al. (2017). Центральным элементом байесовского вывода является теорема Байеса (Wasserman, 2013). В контексте 13 C MFA утверждается, что апостериорное распределение вероятностей потоков θ , обусловленное данными η , p(θ|η), пропорционально вероятности p(η|θ) и априорное распределение потоков p(θ), формализующее соответствующие имеющиеся знания о потоках: (1)
(2006 г.) и Theorell et al. (2017). Центральным элементом байесовского вывода является теорема Байеса (Wasserman, 2013). В контексте 13 C MFA утверждается, что апостериорное распределение вероятностей потоков θ , обусловленное данными η , p(θ|η), пропорционально вероятности p(η|θ) и априорное распределение потоков p(θ), формализующее соответствующие имеющиеся знания о потоках: (1)Здесь все вероятности даны по отношению к конкретной модели Mi, которая выбрана до вывода о потоке.При этом методология логического вывода по существу представляет собой одномодельный подход, основанный на допущении, что известна правильная структура модели.
Именно, модель 13 C MFA Mi состоит из набора метаболических реакций с заданной стехиометрией, связанных с ними атомных переходов и назначений (двух)направленностей реакций, кроме ограничений неравенства на потоки для исключения физиологически бессмысленной системы состояния (Wiechert, 2001). Точнее, реакция может быть либо однонаправленной , если она протекает только в одном направлении, либо двунаправленной , если реагенты обмениваются метками.Следовательно, в то время как скорость однонаправленной реакции полностью характеризуется ее чистым потоком, двунаправленные реакции сопровождаются двумя значениями потока, чистым и обменным потоками (Wiechert and de Graaf, 1997), составляющими вектор потока θ . Здесь чистый поток определяет общую скорость реакции, которая представляет собой разницу между прямым и обратным потоками реакции. Кроме того, обменный поток количественно определяет обмен метками между реагентами (по своей природе неотрицательный), который не обращает внимания на направление.Именно обменный поток определяется как минимум прямого и обратного потоков. Таким образом, однонаправленная реакция характеризуется нулевым обменным потоком.
Точнее, реакция может быть либо однонаправленной , если она протекает только в одном направлении, либо двунаправленной , если реагенты обмениваются метками.Следовательно, в то время как скорость однонаправленной реакции полностью характеризуется ее чистым потоком, двунаправленные реакции сопровождаются двумя значениями потока, чистым и обменным потоками (Wiechert and de Graaf, 1997), составляющими вектор потока θ . Здесь чистый поток определяет общую скорость реакции, которая представляет собой разницу между прямым и обратным потоками реакции. Кроме того, обменный поток количественно определяет обмен метками между реагентами (по своей природе неотрицательный), который не обращает внимания на направление.Именно обменный поток определяется как минимум прямого и обратного потоков. Таким образом, однонаправленная реакция характеризуется нулевым обменным потоком.
В то время как стехиометрия реакции и атомные переходы встречаются в учебниках по биохимии и в базах данных по реакциям, действительно ли обратимая ферментативная реакция протекает одно- или двунаправленно, по существу, зависит от термодинамических движущих сил в условиях in vivo . Поэтому в модели выбор двунаправленности реакции часто не ясен.В этом случае обычно рекомендуется задавать двунаправленную реакцию (Wiechert, 2007).
Поэтому в модели выбор двунаправленности реакции часто не ясен.В этом случае обычно рекомендуется задавать двунаправленную реакцию (Wiechert, 2007).
2.2 Вывод вероятностей двунаправленных реакций
Основополагающее предположение уравнения. (1) заключается в том, что выбранная модель Mi оснащена правильной настройкой двунаправленности реакции. Однако обычно настройка двунаправленности реакции подвержена неопределенности, что означает, что выбор любой конкретной настройки может привести к смещению вывода о потоке. Ввиду конечной цели 13 C MFA, количественного вывода о потоках, желательно признание этих источников неопределенности модели.
Далее вместо одной единственной модели Mi мы рассматриваем модель M как случайную величину с исходами в семействе из 2n моделей {Mi}i, где n — число обратимых реакции (см. Дополнительную информацию S.2 для номенклатуры, используемой повсюду). Каждая модель Mi связана с набором параметров потока θ i . Вероятность того, что k -я реакция (из n обратимых) будет двунаправленной с учетом данных, усредненных по семейству моделей, обозначается p(Δk|η), где Δ k бинарная случайная величина, определяющая, является ли реакция двунаправленной.Для одной модели Mi Δk|Mi равно 0 или 1 в зависимости от того, является ли k -я реакция однонаправленной или двунаправленной соответственно (Δ k полностью определяется исходами M). Апостериорная вероятность p(Δk|η) относится к скольким моделям в семействе {Mi}i реакция является двунаправленной и насколько вероятны эти модели.
Вероятность того, что k -я реакция (из n обратимых) будет двунаправленной с учетом данных, усредненных по семейству моделей, обозначается p(Δk|η), где Δ k бинарная случайная величина, определяющая, является ли реакция двунаправленной.Для одной модели Mi Δk|Mi равно 0 или 1 в зависимости от того, является ли k -я реакция однонаправленной или двунаправленной соответственно (Δ k полностью определяется исходами M). Апостериорная вероятность p(Δk|η) относится к скольким моделям в семействе {Mi}i реакция является двунаправленной и насколько вероятны эти модели.
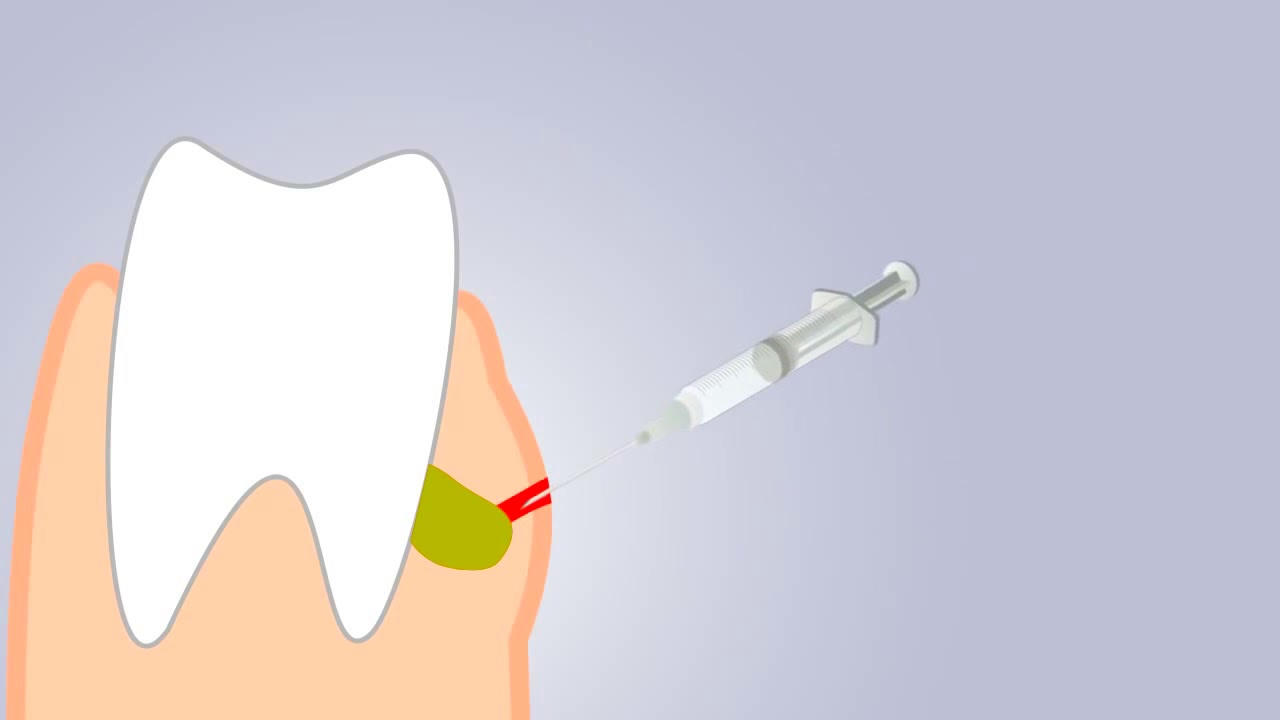 Здесь вероятность того, что k -я реакция будет двунаправленной, p(Δk|η), усредняется по вероятностям ее двунаправленности, определенным для всех одиночных моделей Mi в семействе моделей, Δk|Mi, взвешенных с апостериорными вероятностями одиночных моделей:
Здесь вероятность того, что k -я реакция будет двунаправленной, p(Δk|η), усредняется по вероятностям ее двунаправленности, определенным для всех одиночных моделей Mi в семействе моделей, Δk|Mi, взвешенных с апостериорными вероятностями одиночных моделей:p(Δk|η)=∑ip(Δk|Mi,η)·p(Mi|η)=∑iΔk|Mi·p(Mi|η)
(2)При этом второе равенство следует из определения, p(Δk|Mi,η)=Δk|Mi, так как направленность реакции непосредственно известна из модели.уравнение (2) показывает, откуда берется «усреднение» в BMA: вероятность p(Δk|η) — это среднее значение Δk|Mi, взвешенное с апостериорной вероятностью модели, p(Mi|η). Для расчета усредненных вероятностей направления реакции необходимо определить вероятность p(Mi|η) для каждой модели из модельного семейства {Mi}i. Для расчета этих вероятностей используется теорема Байеса, аналогичная уравнению (1), но для моделей, а не для потоков. Поскольку каждая модель Mi опирается на связанные потоки θ i , мы маргинализируем пространство потоков моделей. Сочетание теоремы Байеса и маргинализации (Wasserman, 2013) приводит к выражению для апостериорной вероятности модели Mi:
Сочетание теоремы Байеса и маргинализации (Wasserman, 2013) приводит к выражению для апостериорной вероятности модели Mi:p(Mi|η)=∫θip(η|θi,Mi)·p(θi|Mi )·p(Mi) dθi∑i∫θip(η|θi,Mi)·p(θi|Mi)·p(Mi) dθi
(3)Для объединенного апостериорного распределения вероятностей p(θi,Mi|η) Байеса ‘ теорема дает:p(θi,Mi|η)=p(η|θi,Mi)·p(θi|Mi)·p(Mi)∑i∫θip(η|θi,Mi)·p(θi| Mi)·p(Mi) dθi
(4) Подставляя уравнение (3) в уравнение (2) (и учитывая, что нормировочные константы идентичны) дает выражение для вероятности k -й реакции быть двунаправленной для модельного семейства {Mi}i:p(Δk|η)=∑iΔk (Mi)∫θip(θi,Mi|η)dθi
(5) В реальных задачах оценка p(Δk|η) в уравнении(5) сводится к вычислению многомерного интеграла. Поскольку интеграл не имеет решения в замкнутой форме, требуется численное приближение. Для аппроксимации апостериорного p(Δk|η) мы используем MCMC, который стохастически генерирует выборки, имитирующие неизвестное распределение вероятностей. Дизайн пробоотборника MCMC представляет собой основное алгоритмическое новшество этой работы, которое подробно описано в Разделе 3.
Прежде чем представить алгоритмические детали, уместно сделать замечание относительно связи между одно- и мультимодельными парадигмами.Апостериорная вероятность модели Mi, p(Mi|η) в уравнении (3) определяется значением функции правдоподобия p(η|θi,Mi) для средних потоков (среднего по отношению к предыдущему, p(θi|Mi), а не для оптимальных значений потоков). Это свойство является недостатком чрезмерно параметризованных моделей, поскольку они чрезмерно гибки и, следовательно, имеют наиболее эффективные наборы параметров, но в среднем показывают низкую производительность (Mackay, 2003). Это связывает вероятность байесовской модели с бритвой Оккама, также известной как принцип экономии, который утверждает, что простые объяснения предпочтительнее более сложных.BMA наследует бритву Оккама от вероятностей модели, поскольку она взвешивает важность каждой модели по ее вероятности. Это признание относится к подходу с одной моделью, описанному во введении, в котором потоки выводятся из сложной «супермодели», в которой все потенциально двунаправленные реакции задаются двунаправленными. Важно отметить, что этот подход с одной моделью не может дать вероятность двунаправленности, поскольку он, рассматривая только одну модель, игнорирует то, что более простые модели более вероятны.Поэтому супермодельный подход не принимает во внимание модельную вероятность и, следовательно, бритву Оккама. Мультимодельный подход через BMA исследует условные вероятности супермодели через модели-кандидаты, где каждая модель-кандидат является экземпляром супермодели с некоторыми обменными потоками, обусловленными нулевым значением.
Важно отметить, что этот подход с одной моделью не может дать вероятность двунаправленности, поскольку он, рассматривая только одну модель, игнорирует то, что более простые модели более вероятны.Поэтому супермодельный подход не принимает во внимание модельную вероятность и, следовательно, бритву Оккама. Мультимодельный подход через BMA исследует условные вероятности супермодели через модели-кандидаты, где каждая модель-кандидат является экземпляром супермодели с некоторыми обменными потоками, обусловленными нулевым значением.
3 алгоритма
Чтобы оценить апостериорное распределение двунаправленности реакции, многомерный интеграл в уравнении.(5) необходимо аппроксимировать численно. Методы MCMC произвели революцию в решении таких проблем (Brooks et al. , 2011). Используя MCMC, интегралы в форме уравнения. (5) аппроксимируются с помощью закона больших чисел (Wasserman, 2013). Это требует, чтобы интеграл был переформулирован в виде ожидания: Затем для аппроксимации апостериорной вероятности двунаправленности реакции, p(Δk|η), генерируются выборки из целевого распределения p(θi,Mi|η). по МЦМС.Согласно закону больших чисел среднее по этим выборкам сходится к желаемому ожидаемому значению в пределе большого размера выборки. В MCMC выборки генерируются путем построения цепи Маркова, которая индуцирует серию эволюционирующих состояний θt,i со стационарным распределением, равным желаемому целевому распределению. Для создания цепи Маркова с целевым распределением p(θi,Mi|η) используется алгоритм Метрополиса-Гастингса (MH) (Брукс и др. , 2011). Алгоритм MH определяется плотностью перехода, индуцирующей цепь Маркова, g и критерием принятия/отклонения, который корректирует индуцированную цепь Маркова, чтобы она имела желаемое стационарное распределение.
по МЦМС.Согласно закону больших чисел среднее по этим выборкам сходится к желаемому ожидаемому значению в пределе большого размера выборки. В MCMC выборки генерируются путем построения цепи Маркова, которая индуцирует серию эволюционирующих состояний θt,i со стационарным распределением, равным желаемому целевому распределению. Для создания цепи Маркова с целевым распределением p(θi,Mi|η) используется алгоритм Метрополиса-Гастингса (MH) (Брукс и др. , 2011). Алгоритм MH определяется плотностью перехода, индуцирующей цепь Маркова, g и критерием принятия/отклонения, который корректирует индуцированную цепь Маркова, чтобы она имела желаемое стационарное распределение.
Для одномодельных целевых распределений с непрерывным пространством состояний доступен ряд эффективных плотностей переходов (Brooks et al., 2011). В этом контексте эффективность означает, что последовательные состояния в цепи Маркова имеют малое время автокорреляции по сравнению со временем вычисления переходов между состояниями. Для мультимодельного случая, рассматриваемого в данной работе, мы должны переходить между модельными пространствами состояний, представленными потоками θ i , используя бинарную индикаторную переменную Δ k .Помните, отличительным свойством семейства моделей {Mi}i является то, что любая двунаправленная реакция вносит вклад в чистый поток и (положительное) значение обменного потока в θ i , в то время как все однонаправленные реакции вносят только один чистый поток ( обменный поток равен нулю). Чтобы сделать состав θ i и его связь со структурой модели явной, в дальнейшем мы обозначаем чистый и обменный потоки модели Mi, ν и ν i соответственно.Здесь при Δ k чистые потоки лишены индекса i , поскольку они присутствуют во всех моделях семейства {Mi}i, а индекс i для обменных потоков ν i подчеркивает, что они относятся к одной модели Mi.
Для мультимодельного случая, рассматриваемого в данной работе, мы должны переходить между модельными пространствами состояний, представленными потоками θ i , используя бинарную индикаторную переменную Δ k .Помните, отличительным свойством семейства моделей {Mi}i является то, что любая двунаправленная реакция вносит вклад в чистый поток и (положительное) значение обменного потока в θ i , в то время как все однонаправленные реакции вносят только один чистый поток ( обменный поток равен нулю). Чтобы сделать состав θ i и его связь со структурой модели явной, в дальнейшем мы обозначаем чистый и обменный потоки модели Mi, ν и ν i соответственно.Здесь при Δ k чистые потоки лишены индекса i , поскольку они присутствуют во всех моделях семейства {Mi}i, а индекс i для обменных потоков ν i подчеркивает, что они относятся к одной модели Mi.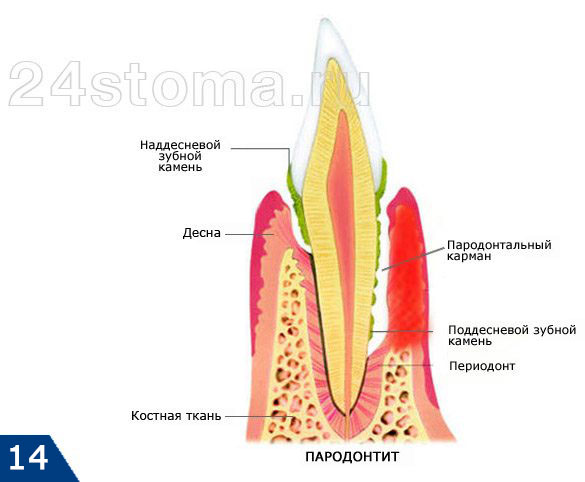 Обратите внимание, что для всего семейства моделей возможен только вывод об общих объектах (чистые потоки ν и двунаправленность реакции Δ k ).
Обратите внимание, что для всего семейства моделей возможен только вывод об общих объектах (чистые потоки ν и двунаправленность реакции Δ k ).
Таким образом, работа цепи Маркова в семействе моделей требует, чтобы плотность перехода учитывала различные размерности пространства состояний в зависимости от настройки двунаправленности (и обменного потока), связанной с состояниями модели.Вычислительная ключевая проблема мультимодельного вывода, возникающая при решении уравнения. (6) представляет собой выборку из совместного апостериорного распределения p(ν,νi,Mi|η) в уравнении. (4). Мы решаем эту проблему, используя RJMCMC (Green, 1995). RJMCMC — это подкласс методов MCMC, предназначенный для построения апостериорных выборок, охватывающих несколько параметрических моделей, вместе с их параметрами, специфичными для модели, путем перехода между моделями в рамках выборки.
3.1 RJMCMC для выборки нескольких моделей
Основным элементом нашего сэмплера RJMCMC для мультимодельного вывода является плотность перехода g для выборки из совместного апостериорного распределения p(ν,νi,Mi|η). Эта переходная плотность RJMCMC g состоит из двух плотностей: плотность g p для специфичного для модели исследования потока, обновляющего векторы потока ν,νi ( внутримодельные скачки ), и плотность g m для исследования модельного пространства, обновляющего пару модель обменного потока νi,Mi ( межмодельные скачки ). Обратите внимание, что как для g p , так и для g m , ν i содержит только обменные потоки, которые являются частью M i , поэтому значение обновления никогда обменный поток выходит за рамки настоящей модели.
Эта переходная плотность RJMCMC g состоит из двух плотностей: плотность g p для специфичного для модели исследования потока, обновляющего векторы потока ν,νi ( внутримодельные скачки ), и плотность g m для исследования модельного пространства, обновляющего пару модель обменного потока νi,Mi ( межмодельные скачки ). Обратите внимание, что как для g p , так и для g m , ν i содержит только обменные потоки, которые являются частью M i , поэтому значение обновления никогда обменный поток выходит за рамки настоящей модели.
Перед детальным обсуждением распределений переходов опишем общую настройку алгоритма RJMCMC (алгоритм 1). Начиная с начальной модели и состояний потока, создается Цепь Маркова состояний νt,νt,i,Mt,i, обозначенная нижним индексом t . Выборка из смешанной переходной плотности RJMCMC г выполняется в два этапа: сначала определяется, взята ли выборка либо из г m , либо из г p с фиксированной вероятностью (Алгоритм 1, L3), затем из выбранного распределения берется меж- или внутримодельная выборка (алгоритм 1, L5, 14).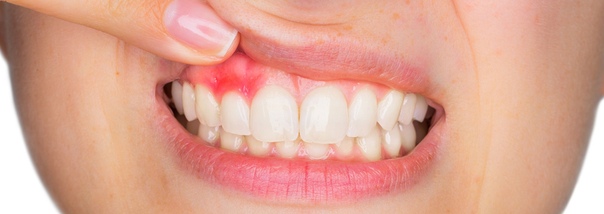
Предлагаемые состояния (обозначенные верхним индексом ★ ) затем принимаются или отклоняются в соответствии с заданными критериями в соответствии со стандартной схемой MH. В нашем случае выдвигаются два критерия отбраковки: один для межмодельных и один для внутримодельных прыжков. Критерии отбраковки зависят от плотностей переходов g m , g p предлагаемых состояний, правдоподобия p(η|ν,νi,Mi), а также априорного p(ν,νi ,Mi) (алгоритм 1, L6, 15 с использованием сокращения z(ν,νi,Mi)=p(η|ν,νi,Mi)·p(ν,νi,Mi)).В зависимости от того, превышает ли значение критерия отклонения α случайное равномерное число u∈[0,1] или нет, предлагаемые состояния либо отвергаются, либо принимаются (алгоритм 1, L8–12, 17–21). В случае принятия предлагаемое состояние является следующим состоянием, в случае отклонения следующее состояние остается идентичным текущему состоянию. Таким образом, N выборок получены для оценки уравнения. (6).
(6).
Алгоритм RJMCMC для 13 C MFA.
3.2
13 C Адаптированные для MFA переходные плотности RJMCMCКлючом к вычислительно эффективному алгоритму RJMCMC является хорошо спроектированная плотность перехода g , которая позволяет цепи Маркова исследовать пространство состояний, так что посещаемые состояния имеют короткое время автокорреляции по сравнению с вычислительными затратами на создание выборок. Здесь желаемое поведение плотности перехода состоит в том, чтобы предложить состояния, которые максимально отличаются от текущего состояния, не вызывая высоких показателей отклонения.Далее мы опишем, как строятся плотности переходов для внутри- и межмодельных прыжков.
Алгоритм 2:Плотность перехода г м для предложений прыжков в цепи Маркова.
3.2.1 Внутримодельная переходная плотность
г р Плотность перехода g p действует на суммарные потоки ν , которые принимают значения в непрерывном пространстве и имеют фиксированное число измерений. Таким образом, она эквивалентна плотности перехода, используемой в Theorell et al. (2017 г.), также используемая в этой работе, которая опирается на классическую плотность перехода «бей-беги» (Bélisle et al. , 1993 г.) для обновления состояний потока ν, νi. Для выбора направления «бей-беги» вероятность направления пропорциональна ширине эллипсоида максимального объема, помещенного в пространство потоков (Zhang and Gao, 2003).
Таким образом, она эквивалентна плотности перехода, используемой в Theorell et al. (2017 г.), также используемая в этой работе, которая опирается на классическую плотность перехода «бей-беги» (Bélisle et al. , 1993 г.) для обновления состояний потока ν, νi. Для выбора направления «бей-беги» вероятность направления пропорциональна ширине эллипсоида максимального объема, помещенного в пространство потоков (Zhang and Gao, 2003).
3.2.2 Плотность межмодельного перехода
г м Основная идея межмодельной плотности г м состоит в том, что модельные скачки предлагаются путем прохождения списка обратимых реакций и изменения некоторых направлений.В контексте 13 C MFA переключение реакции с двунаправленной на однонаправленную эквивалентно уничтожению обмена меткой между пулами субстрата и продукта реакции, т. е. установлению обменного потока на ноль (Wiechert, 2001). Таким образом, в g m модельные переключения вызываются либо преобразованием нулевых обменных потоков в ненулевое значение (называемым активацией направления ), либо обращением ненулевых обменных потоков в ноль (называемым направлением ). деактивация ).В развертываемом нами механизме обновления чистые потоки остаются постоянными при скачках между моделями.
Таким образом, в g m модельные переключения вызываются либо преобразованием нулевых обменных потоков в ненулевое значение (называемым активацией направления ), либо обращением ненулевых обменных потоков в ноль (называемым направлением ). деактивация ).В развертываемом нами механизме обновления чистые потоки остаются постоянными при скачках между моделями.
Для достижения высоких показателей приемлемости предложенная плотность перехода gm(νj★,Mj★|νt,νt,i,Mt,i) сводит к нулю обменные потоки, близкие к нулю. Это приводит только к небольшим изменениям в смоделированных долях маркировки и, следовательно, к небольшим изменениям значения z(ν,νi,Mi), произведения вероятности и априора, что подразумевает высокие показатели приемлемости. Таким образом, вероятность дезактивации k -й реакции состояния t устанавливается равной (νt,i,k/max(νt,i,k))β, где β>0 контролирует скорость дезактивации (алгоритм 2, L4 ).Здесь высокое (низкое) значение для β дает высокую (низкую) скорость дезактивации. Обратите внимание, что после сходимости пробоотборника политика увеличения вероятности деактивации для почти нулевых потоков не оказывает влияния на получаемые апостериорные значения, поскольку увеличение вероятности соответствует увеличению отклонений MH.
Обратите внимание, что после сходимости пробоотборника политика увеличения вероятности деактивации для почти нулевых потоков не оказывает влияния на получаемые апостериорные значения, поскольку увеличение вероятности соответствует увеличению отклонений MH.
Для активации реакций невозможна эвристика, подобная той, что используется для деактивации реакции, поскольку все неактивные обменные потоки равны 0. Поэтому вводится вероятность активации γ∈[0,1] и вероятность возникновения реакция, направленная в Mt,i, чтобы стать двунаправленной в Mj★, устанавливается равной γ (Алгоритм 2, L14).Из-за так называемого согласования размерностей (Грин, 1995) активированные обменные потоки не могут быть инициализированы значением 0, им должно быть присвоено случайное значение из некоторого непрерывного распределения. Поэтому вводится пакт распределения активации (νj,k★), из которого выбираются значения активированных обменных потоков (алгоритм 2, L16).
Важным аспектом алгоритма MH является то, что он требует как прямой вероятности предполагаемого состояния gm(νj★,Mj★|νt,νt,i,Mt,i), так и обратной вероятности текущего состояния gm(νt ,i,Mt,i|νt,νj★,Mj★), при переходе от текущей модели Mt,i к предлагаемой модели Mj★ (Алгоритм 1, L6). Это означает, что необходимо отслеживать изменения двунаправленности. С этой целью введены четыре набора индексов:
Это означает, что необходимо отслеживать изменения двунаправленности. С этой целью введены четыре набора индексов:
L deact : индексы реакций, которые переключаются с двунаправленных в Mt,i на однонаправленные в Mj★| (Алгоритм 2, L6),
L inc : индексы реакций, которые являются двунаправленными в обеих моделях (Алгоритм 2, L8),
L действуют 3 индекса: 9025 действуют от однонаправленного в Mt,i к двунаправленному в Mj★ (Алгоритм 2, L16),
L exc : индексы реакций, которые являются однонаправленными в обеих моделях (Алгоритм 2, L18).
Вероятности перехода назад и вперед рассчитываются путем умножения вероятности всех событий, зарегистрированных наборами индексов. Заметим, что при вычислении обратной вероятности активация и деактивация меняют роли, так как потоки, которые активируются в одном направлении скачка, деактивируются в другом (алгоритм 2, L21–22).
3.3 Детали реализации
Представленный алгоритм RJMCMC для вывода направления реакции из данных маркировки был реализован на C++.Хорошо известно, что методы MCMC рискуют отображать псевдоконвергенцию, то есть состояние, при котором цепь Маркова кажется сошедшейся, но на самом деле исследовала только некоторые целевые режимы (Brooks et al. , 2011). Чтобы сделать цепи Маркова более устойчивыми к псевдосходимости, была использована параллельная закалка с динамическим выбором температуры (Vousden et al. , 2016). Схема параллельного отпуска была распараллелена для повышения вычислительной эффективности. Для моделирования было запущено 30 параллельных цепочек.Чтобы уменьшить влияние начального состояния, всем запускам тестов предшествовал период приработки 10 90 220 5 90 221 выборок. MCMC требует создания большого количества государственных предложений для достижения сходимости цепей Маркова, в реалистичных настройках 13 C MFA до миллионов (Theorell et al. , 2017). Каждое новое состояние требует моделирования фракций маркировки, возникающих из пар модели потока θi,Mi. Для эффективного моделирования сети использовался высокопроизводительный вычислительный пакет 13CFLUX2 (Weitzel et al., 2013). Спецификация модели приведена в формате FluxML (Beyß et al. , 2019).
, 2017). Каждое новое состояние требует моделирования фракций маркировки, возникающих из пар модели потока θi,Mi. Для эффективного моделирования сети использовался высокопроизводительный вычислительный пакет 13CFLUX2 (Weitzel et al., 2013). Спецификация модели приведена в формате FluxML (Beyß et al. , 2019).
Для расчетов параметры (де)активации β и γ были установлены равными 0,1. В качестве распределения активации p act использовалось нормальное распределение, усеченное до [0,1], с нулевым средним значением и стандартным отклонением 0,1. Чтобы избежать изменения априорного объема при переключении между моделями с разным количеством обменных потоков, все обменные потоки преобразуются линейно, чтобы лежать в интервале [0, 1].Влияние этих параметров на производительность алгоритма RJMCMC дополнительно исследуется в исследовании чувствительности параметров (дополнительная информация S.2). Исследование параметров показывает, что производительность RJMCMC относительно нечувствительна к значениям параметров, если избегать экстремального выбора (например, β = 1 или γ = 1).
4 Результаты и обсуждение
Из-за новизны нашего мультимодельного подхода 13 C MFA основной интерес представляют два аспекта:
Вычислительная осуществимость: Многомерный MCMC для традиционного одномодельного вывода о потоках с сетевыми моделями реалистичной сложности требует больших вычислительных ресурсов (Theorell et al., 2017). Мультимодельный подход может чрезмерно увеличить эту высокую вычислительную нагрузку. Таким образом, сначала мы проверяем вычислительную управляемость алгоритма RJMCMC в реалистичном сценарии 13 C MFA. Чтобы получить представление о вычислительной производительности пробоотборника RJMCMC, мы сравнили его с ближайшим опубликованным алгоритмом, а именно с MCMC с одной моделью.
Восстановление двунаправленности реакции: Мы изучаем способность нашего мультимодельного подхода количественно определять вероятность того, что обратимые реакции будут однонаправленными или двунаправленными in vivo .
 Мы делаем это с помощью сетевой модели, типичной для области 13 C MFA, и конфигурации измерения, которая считается передовой (Kappelmann et al. , 2016). Поскольку подход с одной моделью не дает вероятностей двунаправленности реакции (раздел 2.2.1), прямое сравнение результатов подходов с одной и несколькими моделями в этом вопросе невозможно. Таким образом, способность мультимодельного подхода к определению двунаправленности изучается в условиях известного эталонного решения и двух доступных стратегий маркировки.
Мы делаем это с помощью сетевой модели, типичной для области 13 C MFA, и конфигурации измерения, которая считается передовой (Kappelmann et al. , 2016). Поскольку подход с одной моделью не дает вероятностей двунаправленности реакции (раздел 2.2.1), прямое сравнение результатов подходов с одной и несколькими моделями в этом вопросе невозможно. Таким образом, способность мультимодельного подхода к определению двунаправленности изучается в условиях известного эталонного решения и двух доступных стратегий маркировки.
Чтобы продемонстрировать полезность мультимодельного подхода и предлагаемого пробоотборника RJMCMC в этих двух аспектах, мы выбрали реалистичное приложение 13 C MFA с модельным организмом E.coli на основе исследования Crown. и др. (2015). Метаболическая сеть, типичная по своим размерам, включает в себя все основные метаболические пути центрального углеродного метаболизма, сосредоточенного синтеза аминокислот и образования биомассы, поскольку она является репрезентативной для подавляющего большинства исследований в этой области.
Сетевая модель включает 119 метаболитов и 64 реакции, из которых 24 считаются потенциально обратимыми (рис. 1). Из этих 24 потенциально обратимых реакций 23 задаются обратимыми в исходной модели (Crown et al. , 2015). К набору обратимых потоков была добавлена одна дополнительная реакция, поскольку недавно было обнаружено, что она является двунаправленной (Long et al. , 2017). В их первоначальном исследовании было обнаружено, что 18 из 23 обменных потоков практически невозможно идентифицировать, несмотря на обширные наборы измерений, основанные на 14 CLE.Чтобы создать эталонную карту потоков, для чистых потоков (все реакции снабжены чистыми потоками, 8 независимых) наилучшие оценки потоков, представленные Crown et al. (2015). Для обменных потоков 24 потенциально двунаправленные реакции были разделены на две группы (см. рис. 1), 7 де-факто однонаправленных и 17 двунаправленных, в которых все значения обменных потоков были установлены равными 0 и 100 соответственно. Используя эти эталонные потоки, были смоделированы измерения ЖХ-МС/МС в соответствии с установкой, приведенной в (Kappelmann et al., 2016) и оснащен гауссовым шумом (абсолютная погрешность измерения 0,01). Полные спецификации сети и измерений представлены в дополнительной информации S.1.
Используя эти эталонные потоки, были смоделированы измерения ЖХ-МС/МС в соответствии с установкой, приведенной в (Kappelmann et al., 2016) и оснащен гауссовым шумом (абсолютная погрешность измерения 0,01). Полные спецификации сети и измерений представлены в дополнительной информации S.1.
Рис. 1.
Метаболическая сеть центрального углеродного метаболизма штамма E.coli , использованного в данном исследовании. Потенциально двунаправленные реакции делятся на де-факто однонаправленных и двунаправленных реакций, что указывает на их двунаправленность в эталонном растворе. Столбцы показывают апостериорную вероятность двунаправленных реакций для двух сценариев CLE: смесь 20/80 [U- 13 C]- и [ 12 C]-глюкозы и 100% [1,2- 13 C]-глюкозная маркировка.Имена потоков, выделенные жирным шрифтом, соответствуют де-факто однонаправленным реакциям эталонной карты потоков. Вероятность 0,5 означает, что в измерениях не содержится информации о том, является ли реакция однонаправленной или двунаправленной. Спецификация сетевой модели, включая атомные переходы, ограничения и измерения, дана в дополнительной информации S.1
Спецификация сетевой модели, включая атомные переходы, ограничения и измерения, дана в дополнительной информации S.1
Рис. 1.
Метаболическая сеть центрального углеродного метаболизма E.coli , используемая в этом исследовании.Потенциально двунаправленные реакции делятся на де-факто однонаправленных и двунаправленных реакций, что указывает на их двунаправленность в эталонном растворе. Столбцы показывают апостериорную вероятность двунаправленных реакций для двух сценариев CLE: смесь 20/80 [U- 13 C]- и [ 12 C]-глюкозы и 100% [1,2- 13 C]-глюкозная маркировка. Имена потоков, выделенные жирным шрифтом, соответствуют де-факто однонаправленным реакциям эталонной карты потоков.Вероятность 0,5 означает, что в измерениях не содержится информации о том, является ли реакция однонаправленной или двунаправленной. Спецификация сетевой модели, включая атомные переходы, ограничения и измерения, дана в дополнительной информации S. 1
1
4.1 Вычислительная осуществимость алгоритма RJMCMC
Для оценки вычислительной производительности алгоритма выборки RJMCMC его сравнивают с подходом MCMC с одной моделью. Стандартным показателем при сравнении эффективности методов MCMC является относительное ускорение эффективного размера выборки (ESS) (Gilks et al., 1995). Чтобы сделать оба сценария отбора проб MCMC как можно более похожими, пробоотборник MCMC с одной моделью был запущен для модели E.coli , где все потенциально двунаправленные реакции были настроены как двунаправленные. Конвергенция MCMC отслеживалась с помощью чистых потоков, поскольку они являются общими для всех моделей (апостериорные распределения чистых и обменных потоков представлены в дополнительной информации S.2). Минимальный полученный ESS по всем ковариатам после 10 6 отсчетов (сохранялся только каждый сотый отсчет для уменьшения использования дисковой памяти), усредненный по десяти независимым запускам, был записан для обоих пробоотборников. В качестве дополнения к ESS было выполнено несколько тестов сходимости (дополнительная информация S.2). К ним относятся потенциальный коэффициент уменьшения масштаба (PSRF), графики смешения, чтобы показать сходимость непрерывных параметров, и графики дискретного смешения, чтобы показать сходимость в модельном пространстве. Все тесты указывают на сходимость пробоотборника RJMCMC.
В качестве дополнения к ESS было выполнено несколько тестов сходимости (дополнительная информация S.2). К ним относятся потенциальный коэффициент уменьшения масштаба (PSRF), графики смешения, чтобы показать сходимость непрерывных параметров, и графики дискретного смешения, чтобы показать сходимость в модельном пространстве. Все тесты указывают на сходимость пробоотборника RJMCMC.
Пробоотборники MCMC и RJMCMC получили среднее значение ESS 8 ± 2 и 854 ± 128 соответственно, что свидетельствует о том, что пробоотборник RJMCMC обеспечивает примерно 107-кратное повышение качества проб.Каждый из десяти независимых запусков занял в среднем 16,2 и 19,7 ч для MCMC и RJMCMC соответственно по времени настенных часов.
Это замечательная разница в производительности, учитывая, что время до сходимости многих семплеров MCMC, как было показано, увеличивается с увеличением количества измерений (Beskos et al. , 2013; Roberts et al. , 1997). Мы заключаем, что более быстрая сходимость RJMCMC объясняется разницей в размерности, где одиночная модель, используемая для MCMC, имела 32 (8 чистых, 24 обменных) степени свободы (DOF), а модели RJMCMC имели 21. 5 степеней свободы в среднем. Более быстрая сходимость RJMCMC означает, что ускорение, вызванное более низкой размерностью, перевешивает увеличение сложности задачи вывода с несколькими моделями, вызванное множественностью формулировок модели. Таким образом, мы заключаем, что подход с несколькими моделями является вычислительно осуществимым и, кроме того, обеспечивает значительное ускорение по сравнению с подходом с одной моделью.
5 степеней свободы в среднем. Более быстрая сходимость RJMCMC означает, что ускорение, вызванное более низкой размерностью, перевешивает увеличение сложности задачи вывода с несколькими моделями, вызванное множественностью формулировок модели. Таким образом, мы заключаем, что подход с несколькими моделями является вычислительно осуществимым и, кроме того, обеспечивает значительное ускорение по сравнению с подходом с одной моделью.
4.2 Восстановление шагов двунаправленной реакции из
13 C данных После одобрения вычислительной податливости мы оценили способность алгоритма RJMCMC определять, являются ли реакции однонаправленными или двунаправленными на основе имеющихся данных.Особенностью МФА 13 C является то, что выбор изотопно-меченого субстрата, используемого в CLE, решающим образом влияет на качество традиционного вывода о потоке (Crown et al. , 2015; Möllney et al. , 1999). Поэтому мы взяли ту же модель сети и конфигурацию измерения, что и раньше, и рассмотрели две разные входные композиции для мечения: (i) сравнительно дешевая, часто используемая смесь 1:4 однородной [U- 13 C]- и немеченой глюкозы, и (ii) 100% [1,2- 13 C]-глюкоза, которая, как сообщается, более информативна (Crown et al. , 2015).
, 2015).
Применяя алгоритм RJMCMC к сетевой модели, мы получили апостериорную вероятность того, что каждая обратимая реакция будет двунаправленной для обоих наборов меток (рис. 1). Рассматривая реакции, которые были однонаправленными в эталонной карте потоков, но заданы потенциально двунаправленными в модели, GOX1, AA10, PPP6, PPP7, TCA4, AA9 и TCA6 , мы видим, что все потоки, кроме TCA4 и TCA6 были идентифицированы как однонаправленные с высокой достоверностью, независимо от используемого индикатора.Для TCA4 и TCA6 ни один из двух наборов данных не мог сообщить, были ли реакции однонаправленными или двунаправленными, что выражается в промежуточных вероятностях реакций. Реакции EMP2, PPP3, PPP5, PPP8, PPP9, TCA7, TCA8 и TCA9 были правильно идентифицированы как двунаправленные в обоих наборах данных, тогда как EMP4 и EMP5 были правильно идентифицированы как двунаправленные для [1,2- 13 С]-глюкозный индикатор, но еще не определились со смесью индикаторов. Для остальных реакций (все двунаправленные на эталонной карте потоков) в обоих наборах данных отсутствовала информация для классификации однонаправленности или двунаправленности (вероятности от 0,05 до 0,95). Как показано в дополнительной информации S.2, прогоны RJMCMC обладают высокой воспроизводимостью, а также посещают истинную (генерирующую данные) модель несколько раз за прогон. Таким образом, отсутствие идеального восстановления того, является ли реакция двунаправленной, не зависит от алгоритма RJMCMC, но показывает, что информативность измерений недостаточна для подтверждения одно- или двунаправленности реакции.
Для остальных реакций (все двунаправленные на эталонной карте потоков) в обоих наборах данных отсутствовала информация для классификации однонаправленности или двунаправленности (вероятности от 0,05 до 0,95). Как показано в дополнительной информации S.2, прогоны RJMCMC обладают высокой воспроизводимостью, а также посещают истинную (генерирующую данные) модель несколько раз за прогон. Таким образом, отсутствие идеального восстановления того, является ли реакция двунаправленной, не зависит от алгоритма RJMCMC, но показывает, что информативность измерений недостаточна для подтверждения одно- или двунаправленности реакции.
В нашем сценарии нам удалось определить направленность 63 и 54% реакций в зависимости от исходного субстрата. Мы считаем, что это удивительно большая пропорция, поскольку обменные потоки, а вместе с ними и двунаправленность реакций, как известно, трудно идентифицировать (Wiechert and de Graaf, 1997). Это также подчеркивает влияние нашего мультимодельного подхода: реакции, которые остались с неопределенной направленностью, не ограничивают нас в проведении анализа и не заставляют нас делать необоснованные предположения об их направленности. Интересно, что сравнение выбора индикаторов показывает относительно небольшой выигрыш в информации от дорогого индикатора [1,2- 13 C]-глюкозы по сравнению с дешевой смесью немеченой и одинаково меченой глюкозы. Несмотря на то, что эти симуляции выполняются с использованием смоделированных данных, они показывают, какую идентифицируемость мы можем ожидать, используя метод с реальными данными.
Интересно, что сравнение выбора индикаторов показывает относительно небольшой выигрыш в информации от дорогого индикатора [1,2- 13 C]-глюкозы по сравнению с дешевой смесью немеченой и одинаково меченой глюкозы. Несмотря на то, что эти симуляции выполняются с использованием смоделированных данных, они показывают, какую идентифицируемость мы можем ожидать, используя метод с реальными данными.
5 Заключение
В 13 C MFA выводы о потоках in vivo сделаны на основе формулировки модели метаболической сети.Здесь мы выходим за рамки традиционного подхода к выводу о потоках, связанного исключительно с выводом параметров, и вместо этого выполняем одновременный вывод модели и параметра. В частности, мы рассматриваем неопределенность двунаправленности обратимых реакций, возникающую из формулировки обменного потока. Благодаря байесовской парадигме структурные выводы делаются из семейства альтернативных структур моделей, формализованных с использованием усреднения байесовской модели. В вычислительном отношении алгоритм дискретизации RJMCMC строится с адаптированной смешанной плотностью переходов, что позволяет сэмплеру перемещаться по совместному пространству модели-потока.С точки зрения структурных выводов мы показываем, что, используя две разные экспериментальные установки, наш мультимодельный подход обеспечивает статистически надежные выводы без необходимости полного разрешения структуры и без дополнительных вычислительных усилий. Таким образом, BMA, рассчитанный с помощью RJMCMC, позволяет генерировать знания в ситуациях, когда доступных данных недостаточно для полного определения структуры сети. Это актуально не только для 13 C MFA, который был продемонстрирован здесь, но также и для общих условий количественной системной биологии, где модели используются как инструменты измерения.
В вычислительном отношении алгоритм дискретизации RJMCMC строится с адаптированной смешанной плотностью переходов, что позволяет сэмплеру перемещаться по совместному пространству модели-потока.С точки зрения структурных выводов мы показываем, что, используя две разные экспериментальные установки, наш мультимодельный подход обеспечивает статистически надежные выводы без необходимости полного разрешения структуры и без дополнительных вычислительных усилий. Таким образом, BMA, рассчитанный с помощью RJMCMC, позволяет генерировать знания в ситуациях, когда доступных данных недостаточно для полного определения структуры сети. Это актуально не только для 13 C MFA, который был продемонстрирован здесь, но также и для общих условий количественной системной биологии, где модели используются как инструменты измерения.
Благодарности
Авторы выражают благодарность Джонджо Макфаддену за содержательные обсуждения бритвы Оккама и ее связи с BMA, а также Вольфгангу Вихерту за отличные условия работы в IBG-1.
Финансирование
А.Т. поддержан грантом № ЭРА-ИБ-14-81 ДИНАМИКА.
Конфликт интересов : не объявлено.
Каталожные номера
Белиль
С.J.
и др. (1993
)Алгоритмы «бей и беги» для создания многомерных распределений
.Матем. Опер. Рез
.,18
,255
–266
.Бескос
А.
и др. (2013
)Оптимальная настройка гибридного алгоритма Монте-Карло
.Бернулли
,19
,1501
–1534
.Beyß
М.
и др. (2019) Дизайн FluxML: универсальный язык моделирования для анализа метаболических потоков 13 C. Перед. Микробиол ., 10 , 1022.Бреннер
С.
(2010
)Последствия и последствия
.Филос. Транс. Р. Соц. Лонд. Б биол. Науки
. ,
,365
,207
–212
.Брукс
С.
и др. (2011
)Справочник по цепи Маркова Монте-Карло
.Chapman & Hall/CRC Press, Нью-Йорк
.Корниш-Боуден
А.
,Карденас
М.Л.
(2000
) Необратимые реакции в метаболических симуляциях: насколько обратимыми являются необратимые? В: Hofmeyr, J.H. и др. (ред.) Анимация сотовой карты . Издательство Стелленбошского университета, Стелленбос, стр. 65–71.Корона
С.Б.
и др. (2015
)Интегрированный 13 Анализ потока С-метаболизма 14 параллельных экспериментов по мечению в Escherichia coli
.Метаб. Eng
.,28
,151
–158
.Цвийович
М.
и др. (2014
)Преодоление пробелов в системной биологии
.мол. Жене. Геномика
,289
,727
–734
.Gilks
W. R.
R.
1995
)Цепь Маркова Монте — Карло на практике
.Chapman & Hall/CRC Press, Бока-Ратон
.Зеленый
С.Дж.
(1995
)Обратный скачок Расчет цепи Маркова методом Монте-Карло и определение байесовской модели
.Биометрика
,82
,711
–732
.Hoeting
J.A.
и др. (1999
)Усреднение байесовской модели: учебное пособие
.Стат.
.,14
,382
–401
.Кадиркаманатан
В.
и др. (2006
)Цепь Маркова Монте-Карло Алгоритм анализа распределения метаболических потоков на основе Corynebacterium glutamicum
.Биоинформатика
,22
,2681
–2687
.Kappelmann
J.
и др. (2016
)Разрубая гордиев узел: идентификация анаплеротических реакций у Corynebacterium glutamicum с помощью анализа 13 С-метаболического потока
.
Биотехнология. Биоэнг
.,113
,661
–674
.Кирк
П.
и др. (2015
)Системная биология (не)определенность
.Наука
,350
,386
–388
.Кремлинг
А.
(2013
)Системная биология: математическое моделирование и модельный анализ
.Chapman & Hall/CRC Press, Бока-Ратон
.Kuepfer
L.
и др. (2007
)Моделирование ансамбля для анализа динамики передачи сигналов клетками
.Нац. Биотехнолог
.,25
,1001.
Лю
Ю.
и др. (2015
)ИСКУПЛЕНИЕ: моделирование ансамбля уменьшенной размерности и оценка параметров
.Биоинформатика
,31
,3387
–3389
.Длинный
C.P.
и др. (2017
)Фермент I способствует обратному переходу от пирувата к фосфоенолпирувату в Escherichia coli
.
Нац. Коммуна
.,8
,14316.
Маккей
Д.Дж.
(2003
)Теория информации, логические выводы и алгоритмы обучения
.Издательство Кембриджского университета
,Кембридж
.Мишкович
Л.
,Хатзиманикатис
В.
(2011
)Моделирование неопределенностей биохимических реакций
.Биотехнология. Биоэнг
.,108
,413
–423
.Мёлльни
М.
и др. (1999
)Двунаправленные этапы реакции в метаболических сетях: IV. Оптимальный план экспериментов по мечению изотопомеров
.Биотехнология. Биоэнг
.,66
,86
–103
.Оутс
CJ
и др. (2014
)Вывод причинно-следственной сети с использованием биохимической кинетики
.Биоинформатика
,30
,i468
–74
.Риш
И.
,Грабарник
Г.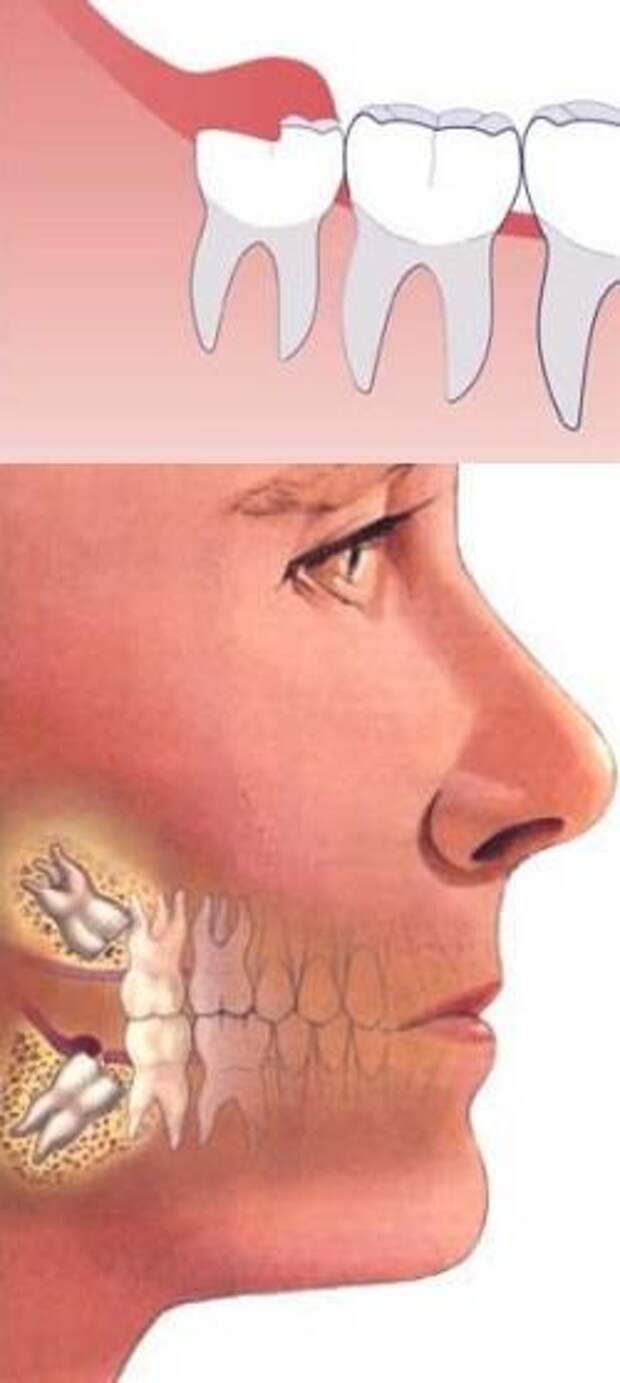
2014
)Разреженное моделирование: теория, алгоритмы и приложения
.CRC Press, Бока-Ратон
.Roberts
GO
и др. (1997
)Слабая сходимость и оптимальное масштабирование алгоритмов случайных блужданий Метрополиса
.Энн. заявл. Вероятно
.,7
,110
–120
.Teusink
B.
и др. (2000
)Можно ли понять дрожжевой гликолиз с точки зрения кинетики входящих в его состав ферментов in vitro? Тестирование биохимии
.евро. J. Biochem
.,267
,5313
–5329
.Theorell
A.
и др. (2017
)Чтобы быть уверенным в неопределенности: байесовская статистика для 13 C Анализ метаболических потоков
.Биотехнология. биоинж.
,114
,2668
–2684
.Timonen
J.
и др. (2018
) Вероятностная основа для вывода о структуре молекулярной сети посредством механистического моделирования. В: IEEE/ACM Transactions по вычислительной биологии и биоинформатике.
В: IEEE/ACM Transactions по вычислительной биологии и биоинформатике. Тони
Т.
и др. (2009
)Приближенная байесовская схема вычислений для вывода параметров и выбора модели в динамических системах
.JR Soc. Интерфейс
,6
,187
–202
.Тран
Л. М.
и др. (2008
)Ансамбльное моделирование метаболических сетей
.Биофиз. J
.,95
,5606
–5617
.Туммлер
К.
,Клипп
Э.
(2018
)Несоответствие между данными и ожиданиями в отношении метаболических моделей: как сопоставить эксперименты и вычислительные усилия, чтобы получить количественные прогнозы
.Курс. мнение Сист. Биол
.,8
,1
–6
.Vousden
W.
и др.(2016
)Динамический выбор температуры для параллельного отпуска в моделировании методом Монте-Карло цепи Маркова
.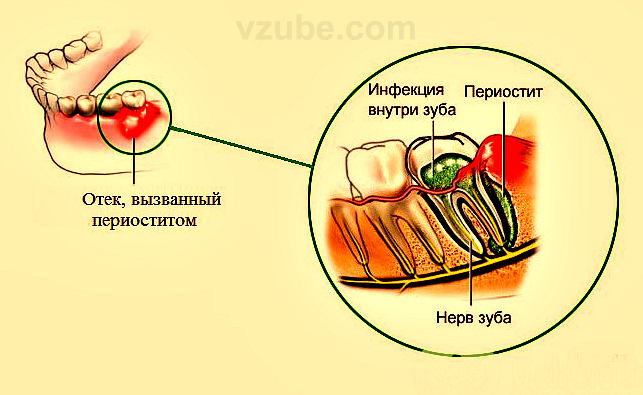
Пн. Заметки Р. Астрон. Соц
.,455
,1919
–1937
.Вышемирский
В.
,Джиролами
М.А.
(2008
)Байесовское ранжирование моделей биохимических систем
.Биоинформатика
,24
,833
–839
.Wasserman
L.
(2013
)Вся статистика: краткий курс статистических выводов
.Springer Science & Business Media, Нью-Йорк
.Weitzel
М.
и др. (2013
)13CFLUX2 — пакет высокопроизводительного программного обеспечения для 13 C-Metabolic Flux Analysis
.Биоинформатика
,29
,143
–145
.Вихерт
В.
(2001
)13 C анализ метаболических потоков
.Метаб. Eng
.,3
,195
–206
.Вихерт
В.
(2007
)Термодинамический смысл метаболических обменных потоков
.
Биофиз. J
.,93
,2255
–2264
.Wiechert
W.
,de Graaf
A.A.
(1997
)Этапы двунаправленной реакции в метаболических сетях: I.Моделирование и имитация экспериментов по мечению изотопов углерода
.Биотехнология. Биоэнг
.,55
,101
–117
.Zamboni
N.
и др. (2009
)13 Анализ метаболических потоков на основе C
.Нац. Протокол
.,4
,878
–892
.Чжан
Ю.
,Гао
Л.
(2003
)О численном решении задачи на эллипсоид максимального объема
.SIAM J. Optim
.,14
,53
–76
.© Автор(ы), 2019. Опубликовано Oxford University Press. Все права защищены. Для разрешений, пожалуйста, по электронной почте: [email protected]
.



 Он формируется в течение 10 дней.
Он формируется в течение 10 дней. Появляется из-за:
Появляется из-за:
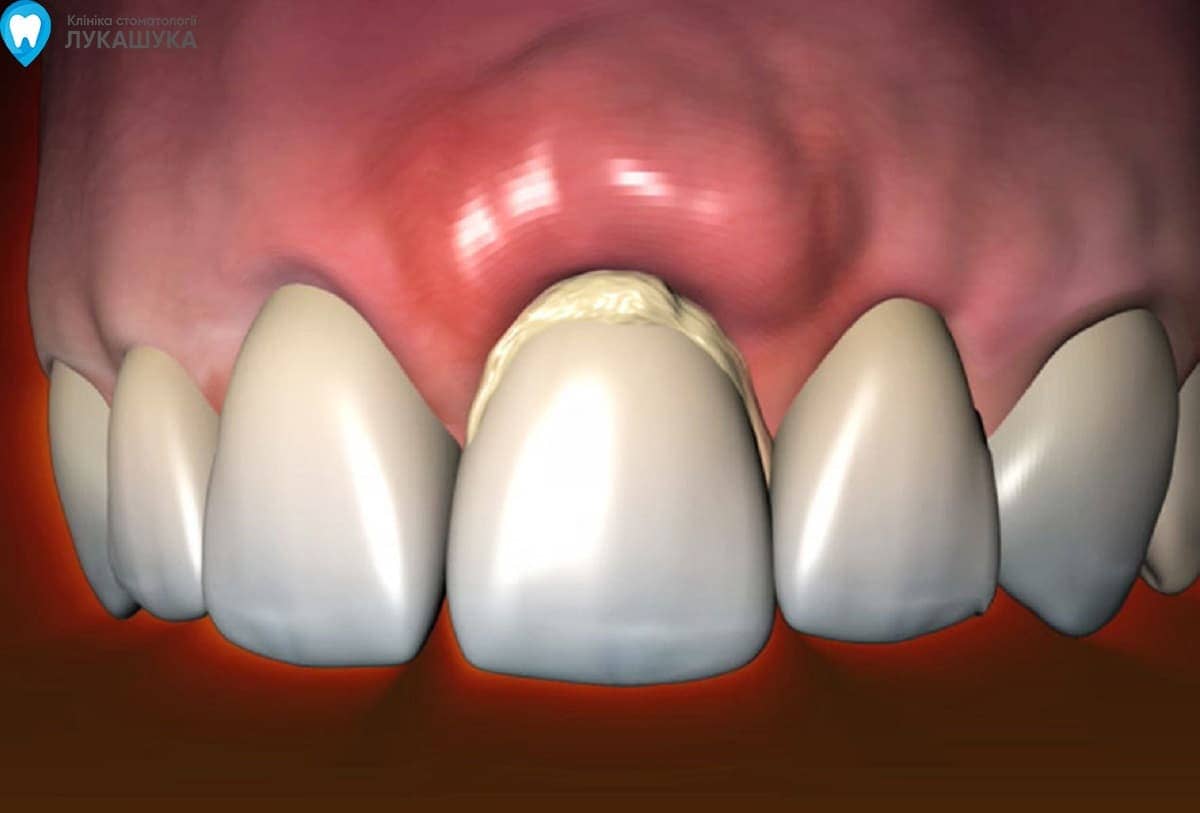
 Показан прием обезболивающих препаратов по назначению врача. Непроходящая боль может свидетельствовать о развитии воспалительного процесса, повреждении нерва.
Показан прием обезболивающих препаратов по назначению врача. Непроходящая боль может свидетельствовать о развитии воспалительного процесса, повреждении нерва.

 Мы делаем это с помощью сетевой модели, типичной для области 13 C MFA, и конфигурации измерения, которая считается передовой (Kappelmann et al. , 2016). Поскольку подход с одной моделью не дает вероятностей двунаправленности реакции (раздел 2.2.1), прямое сравнение результатов подходов с одной и несколькими моделями в этом вопросе невозможно. Таким образом, способность мультимодельного подхода к определению двунаправленности изучается в условиях известного эталонного решения и двух доступных стратегий маркировки.
Мы делаем это с помощью сетевой модели, типичной для области 13 C MFA, и конфигурации измерения, которая считается передовой (Kappelmann et al. , 2016). Поскольку подход с одной моделью не дает вероятностей двунаправленности реакции (раздел 2.2.1), прямое сравнение результатов подходов с одной и несколькими моделями в этом вопросе невозможно. Таким образом, способность мультимодельного подхода к определению двунаправленности изучается в условиях известного эталонного решения и двух доступных стратегий маркировки.